00_算法学习

About 4 minstudyalgorithm

一、基本概念

  • 算法: 同一个问题的不同解决方法,算法往往是针对特定数据结构的

  • 时间测量：计算算法时间差、幅度不够循环来凑(扩大数据量)

  • 空间测算: 数据占用的空间越小越好

  • 常数时间操作：执行时间固定的都是常数操作（算数运算、位运算、赋值、比较、数组寻址）。 反之执行时间不固定的操作都不是常数时间的操作（链表寻址去取数）

  • 时间复杂度（最重要的指标）：算法的时间复杂度随着规模的增加，算法运行的时间增长率，通常用大O标记

    • 标记解释描述
      O(1)常数阶算法的运行时间不随输入的规模增加而变化，例如查找数组中的第一个元素
      O(logN)对数阶运行时间随着数据增加而相对较慢增长，例如二分查找。循环次数是n/2（从数组的中间选择一个随机点进行查找，然后重复这个过程）
      O(n)线性阶时间随着n的变化而线性变化（随着处理数据量的增加，处理时间也会增加）。比如遍历数组中的所有元素
      O(N*logN)线性对数阶算法的运行时间随着输入规模略微快于线性增长，如快速排序。将O(logN)循环n次
      O(N^2)平方阶算法的运行时间随着输入规模呈平方级别增长，例如冒泡排序和插入排序。O(n)嵌套循环2次
      O(N^3)立方阶嵌套3次循环n次
      O(N^k)K次方阶嵌套n次循环
      O(2^N)指数阶算法的运行时间随着输入规模呈指数级别增长，例如求解汉诺塔问题。时间根据数量指数增长
    • // O(n)
for(int i=0; i<3; i++) {
	System.out.println(i);
}
// O(n^2)
int[] arr = [1,2,3];
for(int i=0; i<3; i++) {
	for(int j; j < 3; j++) {
    System.out.println(arr[j]);
  }
}

  • 额外空间复杂度：除开出参和入参的空间外，额外需要开辟空间去处理的称为额外空间

    • 标记解释描述
      O(1)常数阶没有循环
      O(n)线性阶时间随着n的变化而变化
      O(n^2)平方阶嵌套O(n)

  • 常数项：随机数数据直接测试

  • 最优解：时间复杂度尽量低、空间复杂度尽量低。常数间操作优化不纳入最优解

  • 对数器：用来验证自己的算法，对数器是特别重要的，写对数器的过程就是练习coding能力的时候。大样本随机测试，检查算法是否正确，用足够多的样本和正确的算法计算结果样本去对比被验证的算法结果(用已有的排序算法和自己写的排序算法都去处理数据，之后将处理的结果对比一下是否一致)

  • 二分法：每次把数据分为两份处理。O(logn)

二、数据结构的三要素

1、数据的逻辑结构

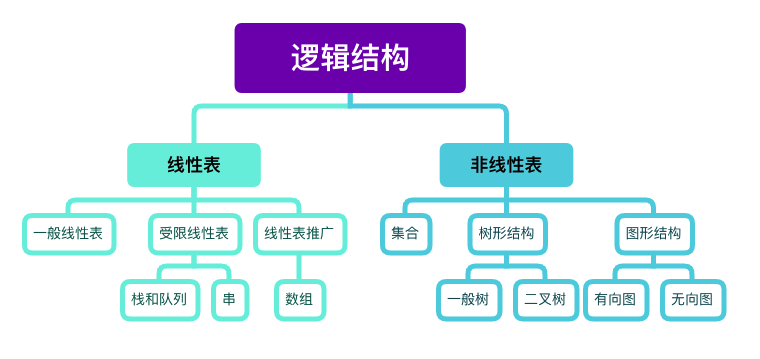
数据的逻辑结构分类图

集合、线性结构、树形结构、网状结构（图）

2、数据的存储结构

顺序存储：逻辑上相邻的结构在物理上也是相邻的

链式存储：通过元素指针表示程序的逻辑结构

散列表存储：顺序存储+散列（通过关键字计算hash值）

索引存储：顺序存储+索引（通过关键字建立索引表）

3、数据的运算

运算包括运算定义和实现： 定义针对逻辑结构，指出元算的功能。实现针对存储结构，指出运算的具体操作步骤。

三、五个重要特性和好算法

1、有穷性：算法在又穷个步骤能执行完，每个步骤在有穷时间内执行完

2、确定性：每条指令都有确切的含义，相同的输入有相同的输出

3、可行性：可以通过已有的基本运算执行有限次完成

4、输入：有零个或多个输入

5、输出：有零个或多个输出

好的算法应该达到以下目标：

  1. 正确：能够正确的解决问题
  2. 可读性：可以阅读，帮助人们理解
  3. 健壮性：非法数据输入时，能够做出反应而不致于产生莫名其妙的错误
  4. 高效率和低存储：执行时间（时间复杂度）和存储空间（空间复杂度）要尽可能小，一般都与数据规模有关
Last update:
Contributors: gaoqisen