02_排序算法学习

一、选择排序O(n^2)-无稳定性

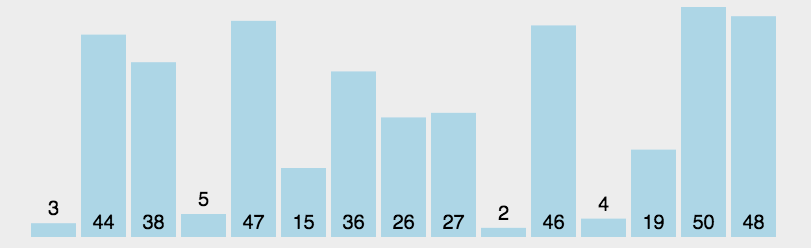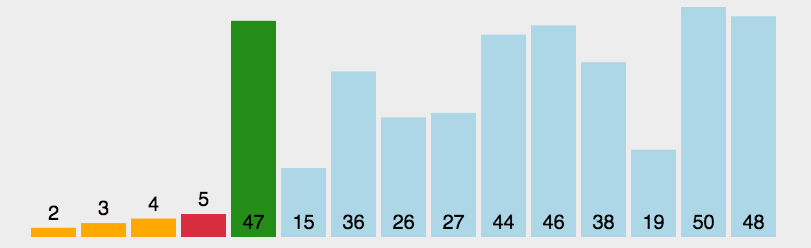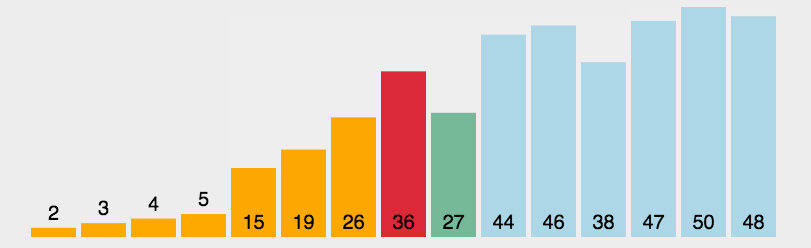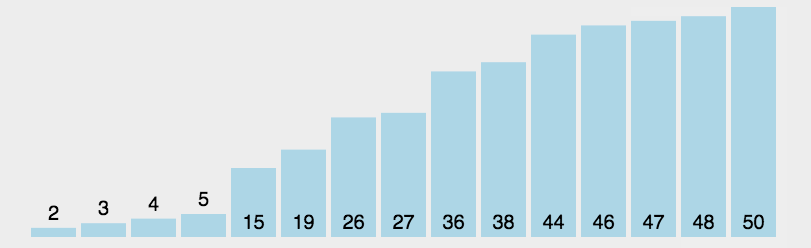
先找到最小的数字然后把它放在列表的最前面。最简单最没用的排序算法，有优化空间,不稳定。原理是找到最小的数把它放在最前面。

public static void main(String[] args) {
        int[] arr = {8,6,5,4,7,1,2,3,2};

        // 排序算法，每次找到最小的数字放在最前面
        for (int i = 0; i< arr.length - 1; i++) {
            int minVal = i;
            // 找到最小数字的下标
            for(int j = i+1; j < arr.length; j++) {
                if(arr[j] < arr[minVal]) {
                    minVal = j;
                }
            }

            // 将最小的数字放在最前面
            int tmp = arr[minVal];
            arr[minVal] = arr[i];
            arr[i] = tmp;
        }

        // 遍历数组
        for (int i = 0; i< arr.length; i++) {
            System.out.println(arr[i]);
        }
    }

二、 冒泡排序

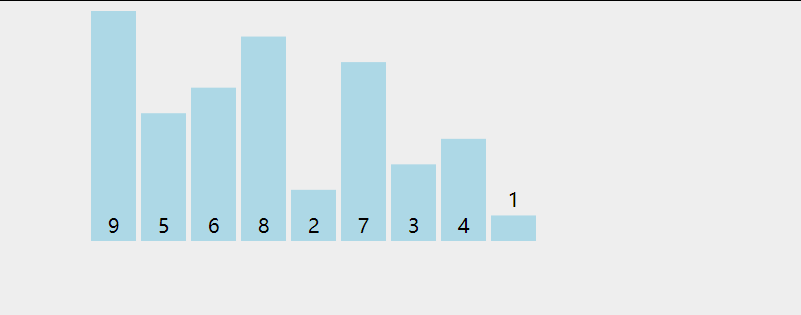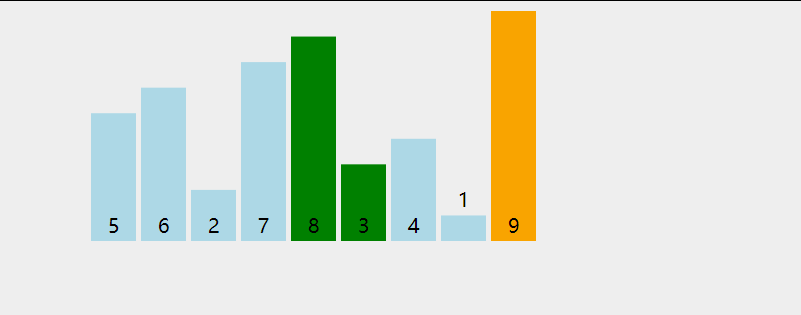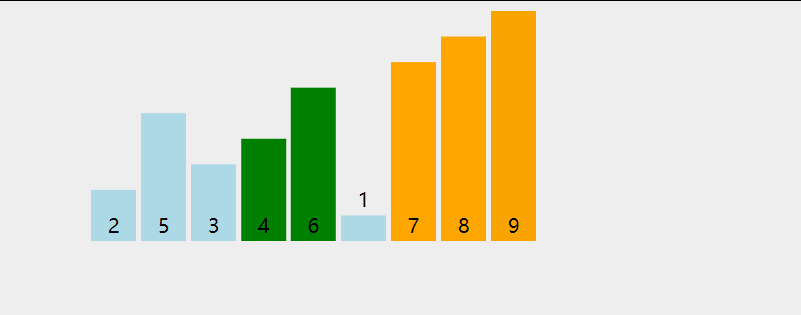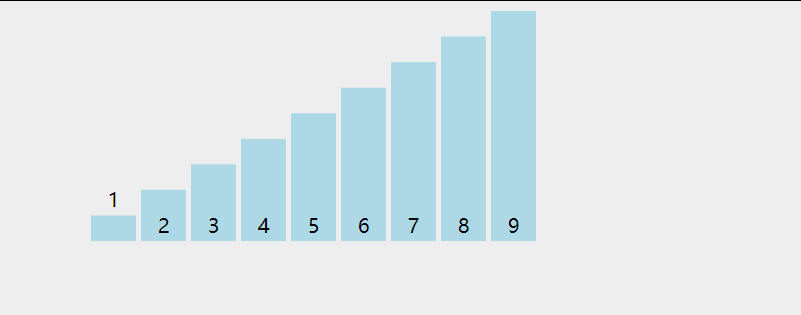
从无序序列头部开始，进行两两比较，根据大小交换位置，直到最后将最大（小）的数据元素交换到了无序队列的队尾，从而成为有序序列的一部分；下一次继续这个过程，直到所有数据元素都排好序

public class BubbleSort {

    public static void main(String[] args) {
        int[] a = {9,6,5,2,3,4,80,7,1,10};
        for (int i = 0; i < a.length; i++) {
            for (int j = 1; j < a.length; j++) {
                int index = j-1;
                if(a[index] > a[j]) {
                    swap(a, index, j);
                }
            }
        }

        // 输出
        for (int i = 0; i < a.length; i++) {
            if(i == (a.length - 1)){
                System.out.print(a[i]);
                break;
            }
            System.out.print(a[i]+ ", ");
        }
        System.out.println("");
    }

    static void swap(int[] a, int start, int end) {
        int temp = a[start];
        a[start] = a[end];
        a[end] = temp;
    }
}

三、 插入排序

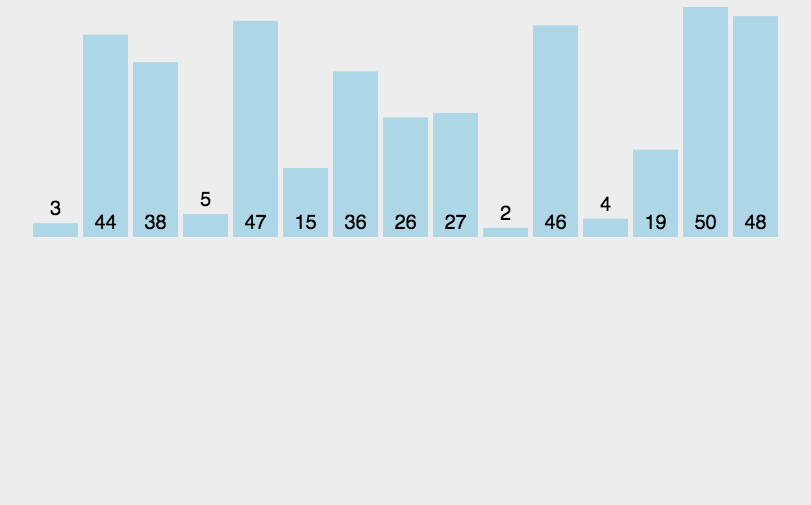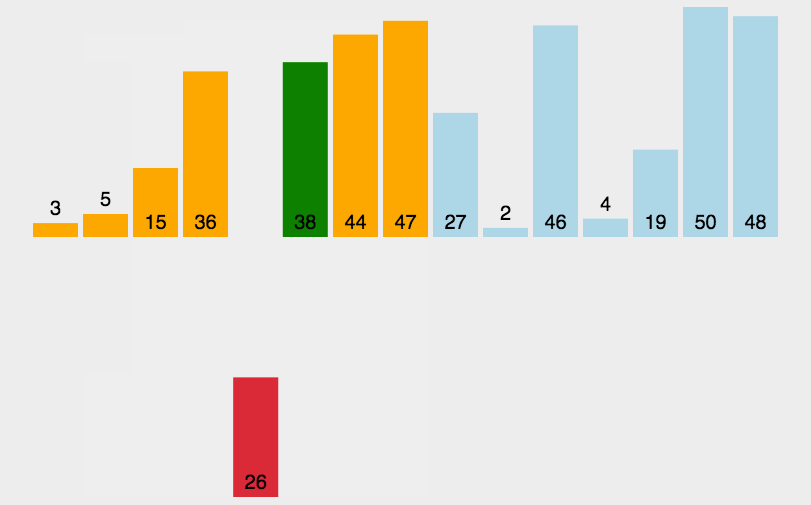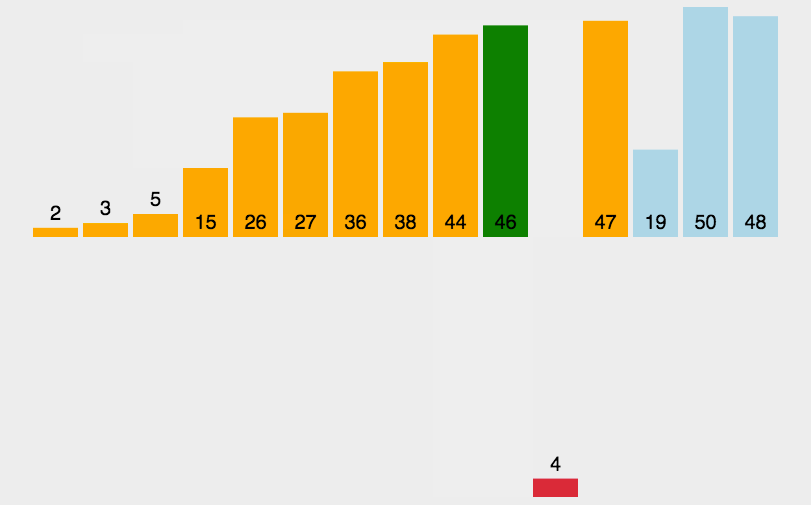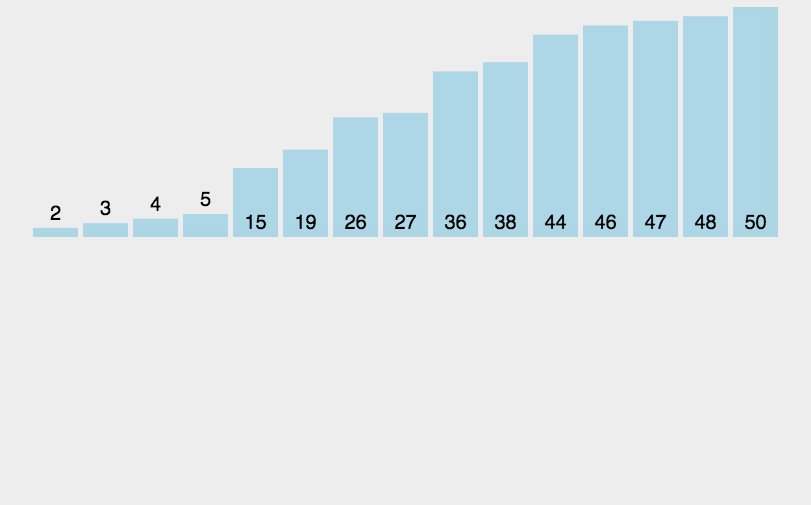
插入排序是一种简单直观的排序算法。它的基本思想是拿到当前值之后往前面的正确位置移动。

// 插入排序
public class InsertionSort {

    public static void main(String[] args) {
        int[] a = {9,6,5,2,3,4,80,7,1,10};

        for (int i = 0; i < a.length; i++) {
            // 通过当前值和前面的值比较，并把当前值放到恰当的位置
            for (int j = i; j > 0; j--) {
                if(a[j] < a[j-1]) {
                    swap(a, j, j-1);
                }
            }
        }

        print(a);

    }
    // 替换
    static void swap(int[] a, int start, int end) {
        int temp = a[start];
        a[start] = a[end];
        a[end] = temp;
    }
    static void print(int[] a) {
        // 输出
        for (int i = 0; i < a.length; i++) {
            if(i == (a.length - 1)){
                System.out.print(a[i]);
                break;
            }
            System.out.print(a[i]+ ", ");
        }
        System.out.println("");
    }

}

四、希尔排序-无稳定性

A video

将数组分为几段处理，比如15个数组元素分为每4个一组进行插入排序，之后在进行2个一组插入排序，之后在进行1个一组进行插入排序就可以了。这样缩短了数字之间的插入排序。希尔排序是不常用的排序方法。

// 希尔排序
public class ShellSort {

    public static void main(String[] args) {
        int[] a = {9,6,5,2,3,4,80,7,1,10};

        // knuth序列
        int h = 1;
        while( h <= a.length / 3) {
            h = h*3 +1;
        }

        for (int gap = h; gap > 0; gap = (gap -1)/3) {
            for (int i = gap; i < a.length; i++) {
                for (int j = i; j > gap -1 ; j-=gap) {
                    if(a[j] < a[j-gap]) {
                        swap(a, j, j-gap);
                    }
                }
            }
        }

        print(a);

    }

    static void swap(int[] a, int start, int end) {
        int temp = a[start];
        a[start] = a[end];
        a[end] = temp;
    }
    static void print(int[] a) {
        // 输出
        for (int i = 0; i < a.length; i++) {
            if(i == (a.length - 1)){
                System.out.print(a[i]);
                break;
            }
            System.out.print(a[i]+ ", ");
        }
        System.out.println("");
    }

}

五、快速排序-无稳定性

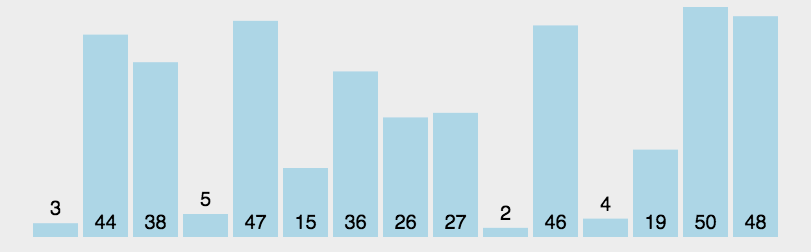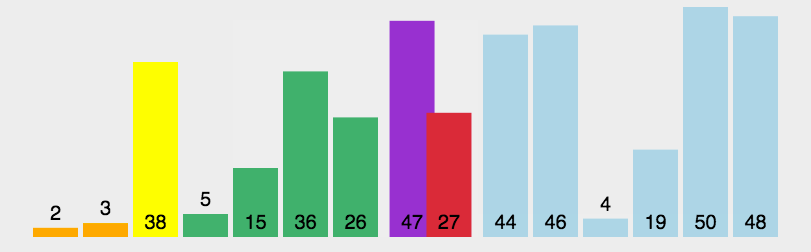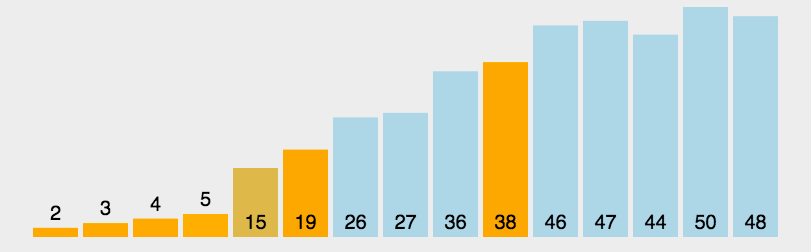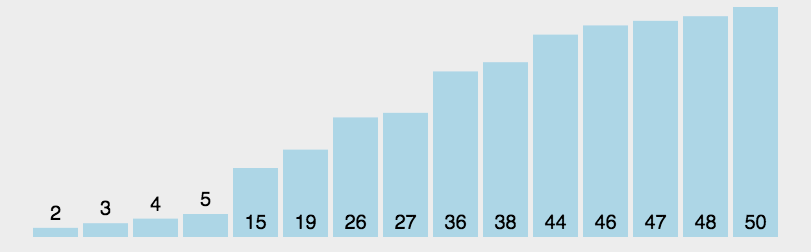
1、单轴排序

// 快速排序: 采用不断的比较和移动来实现排序
// 对于给定的一组记录，选择一个基准元素,通常选择第一个元素或者最后一个元素,通过一趟扫描，
// 将待排序列分成两部分,一部分比基准元素小,一部分大于等于基准元素,此时基准元素在其排好序
// 后的正确位置,然后再用同样的方法递归地排序划分的两部分，直到序列中的所有记录均有序为止。
public class QuickSort {

    public static void main(String[] args) {
        int[] arr = { 6, 5, 9, 8, 3, 2, 1, 7, 10};
        sort(arr);
        print(arr);
    }

    // 排序
    static void sort(int[] arr) {
        partition(arr, 0, arr.length-1);
    }

    // 分区
    static void partition(int[] arr, int left, int right){
        if(left >= right) {
            return;
        }
        // 指针指向左边的第一个值
        int i = left;
        // 已右边的数为基数(轴)
        int temp = arr[right];
        // 右边的指针就是right-1
        int j = right;

        // 当左边的值小于右边值的时候
        while (i < j) {
            // 从左往右找大于或者基数的数字，并移动到arr.length-1的位置
            while (i<j && arr[i] <= temp) {
                i++;
            }
            if(i < j) {
                arr[j--] = arr[i];
            }
            // 从有右往左找小于或者等于基数的数字，并移动数字到i++的位置
            while (i<j && arr[j] > temp){
                j--;
            }
            if(i < j) {
                arr[i++] = arr[j];
            }
        }
        // 将基数放在i的位置
        arr[i] = temp;
        // 递归循环轴左边的值
        partition(arr, left, i-1);
        // 递归循环轴右边的值
        partition(arr, i+1, right);
    }



    static void swap(int[] a, int start, int end) {
        int temp = a[start];
        a[start] = a[end];
        a[end] = temp;
    }
    static void print(int[] a) {
        // 输出
        for (int i = 0; i < a.length; i++) {
            if(i == (a.length - 1)){
                System.out.print(a[i]);
                break;
            }
            System.out.print(a[i]+ ", ");
        }
        System.out.println("");
    }
}

2、荷兰国旗

荷兰国旗包含三种颜色红、白、蓝，应用在数组排序中就是小于、等于、大于。

1、小于等于指定数放左边，大于指定数放右边

题目1：将给定的数组如：[2,5,7,3,4,9,10]，按照指定数如5，小于等于指定数的放左边，大于指定数的放右边。不用用扩展数组。O(n)

解：通过左边区域下标(L)控制，小于等于指定数字的交换数字后L并往后跳，大于的L往后跳

// 思路
// 1、用最右边的数作为参考值进行排序
//   a、用两个指针控制区域(从-1开始)和当前比较位置
//   b、判断如果当前值小于参考值则交换位置
//   c、交换参考值到当前位置
// 2、用最右边的参考值的下标左边递归排序
// 3、用最右边的参考值的下标右边递归排序

private static void sort(int[] arr) {
        if(arr == null || arr.length < 2) {
            return;
        }

        process(arr, 0, arr.length -1);
    }

    private static void process(int[] arr, int l, int r) {
        if(l >= r) {
            return;
        }

        int m = partition(arr, l, r);
        process(arr, l, m - 1);
        process(arr, m + 1, r);
    }

    private static int partition(int[] arr, int l, int r) {
        if(l > r) {
            return -1;
        }
        if(l == r) {
            return l;
        }
        int current = l;
        int leftArea = l-1;
        while (current < r) {
            if(arr[current] <= arr[r]) {
                swap(arr, current, ++leftArea);
            }
            current++;
        }
        swap(arr, r, ++leftArea);
        return leftArea;
    }

    private static void swap(int[] arr, int i, int j) {
        if(i == j) {
            return;
        }
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

2、小于放左边，等于指定数放中间，大于放右边

题目二：将给定的数组如：[2,5,7,3,4,9,10]，按照指定数如5，小于指定数的放左边，等于指定数的放中间，大于指定数的放右边。不用用扩展数组。O(n)

解：通过左边区域下标(L)和右边区域R控制，小于指定数字的交换数字后L并往后跳，大于的R交换数字后往前跳

思路：主要就是已最右边的数为基数，小于基数的放左边，等于基数的放中间，大于基数的放右边。之后递归处理依次排序左右两边即可。

    private static void sort(int[] arr) {
        if(arr == null || arr.length < 2) {
            return;
        }

        process(arr, 0, arr.length -1);
    }

    private static void process(int[] arr, int l, int r) {
        if(l >= r) {
            return;
        }

        int[] m = partition(arr, l, r);
        process(arr, l, m[0] - 1);
        process(arr, m[1] + 1, r);
    }

    // 荷兰数组，小于 等于 大于。 返回中间值的边界
    private static int[] partition(int[] arr, int l, int r) {
        if(l > r) {
            return new int[]{-1, -1};
        }
        if(l == r) {
            return new int[]{l, r};
        }
        int leftArea = l - 1;
        int rightArea = r;
        int index = l;
        while (index < rightArea) {
            // 当前值等于右边的基准值则当前值往后移
            if(arr[index] == arr[r]) {
                index++;
                continue;
            }
            // 当前值小于右边的基准值则左区域值+1后和当前值替换，然后当前值+1
            if(arr[index] < arr[r]) {
                swap(arr, ++leftArea, index++);
                continue;
            }
            // 当前值大于右边的基准值则当前值和右区域往左移后替换，替换后当前值重新比
            swap(arr, --rightArea, index);
        }
        swap(arr, r, rightArea);
        return new int[]{leftArea, rightArea};
    }

    private static void swap(int[] arr, int i, int j) {
        if(i == j) {
            return;
        }
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

3、标准的荷兰国旗排序（随机快排）

和第二个版本对比只是多了一个随机数去定位基准数

优势：

• 划分值越在中间性能越好，第二种的划分值是固定右侧。
• 随机划分值是将好事件和差事件变为概率事件
• 概率都是1/N, 所有情况都考虑这种概率模型就是长期期望。时间复杂度O(N*logN),额外空间复杂度O(logN)

private static void sort(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        process(arr, 0, arr.length - 1);
    }

    private static void process(int[] arr, int l, int r){
        if(l >= r) {
            return;
        }
        // 和第二个版本对比只是多了一个随机数去定位基准数
        swap(arr, l + (int) (Math.random() * (r - l + 1)), r);
        int[] m = partition(arr, l, r);
        process(arr, l, m[0] - 1);
        process(arr, m[1] + 1, r);
    }

    public static int[] partition(int[] arr, int l, int r) {
        if(l == r) {
            return new int[]{l, r};
        }

        if(l > r) {
            return new int[]{-1, -1};
        }

        int leftArea = l -1;
        int rightArea = r;
        int index = l;
        while (index < rightArea) {
            if(arr[index] == arr[r]) {
                index++;
                continue;
            }
            if(arr[index] < arr[r]) {
                swap(arr, index++, ++leftArea);
                continue;
            }
            swap(arr, index, --rightArea);
        }
        swap(arr, rightArea, r);
        return new int[]{leftArea + 1, rightArea};
    }


    private static void swap(int[] arr, int i, int j) {
        if(i == j) {
            return;
        }
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

4、非递归的快排(栈+荷兰国旗)

    private static void sort(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        process(arr, 0, arr.length - 1);
    }
    
    private static void process(int[] arr, int l, int r){
        if(l >= r) {
            return;
        }
        swap(arr, l + (int) (Math.random() * (r - l + 1)), r);
        int[] m = partition(arr, l, r);
        // 下面的代码替代了递归
        Stack<StackTmp> stack = new Stack<>();
        stack.push(new StackTmp(l, m[0] -1));
        stack.push(new StackTmp(m[0] + 1, r));

        while (!stack.isEmpty()) {
            StackTmp pop = stack.pop();
            if(pop.l < pop.r) {
                swap(arr, pop.l + (int) (Math.random() * (pop.r - pop.l + 1)), pop.r);
                int[] range = partition(arr, pop.l, pop.r);
                stack.push(new StackTmp(pop.l, range[0] - 1));
                stack.push(new StackTmp(range[1] + 1, pop.r));
            }
        }
    }

    public static int[] partition(int[] arr, int l, int r) {
        if(l == r) {
            return new int[]{l, r};
        }
        if(l > r) {
            return new int[]{-1, -1};
        }

        int leftArea = l -1,rightArea = r,index = l;
        while (index < rightArea) {
            if(arr[index] == arr[r]) {
                index++;
                continue;
            }
            if(arr[index] < arr[r]) {
                swap(arr, index++, ++leftArea);
                continue;
            }
            swap(arr, index, --rightArea);
        }
        swap(arr, rightArea, r);
        return new int[]{leftArea + 1, rightArea};
    }
    private static void swap(int[] arr, int i, int j) {
        if(i == j) {
            return;
        }
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
    
class StackTmp{
    public int l;
    public int r;
    public StackTmp(int l, int r) {
        this.l = l;
        this.r = r;
    }
}

5、非递归的快排(队列+荷兰国旗)

    private static void process(int[] arr, int l, int r){
        if(l >= r) {
            return;
        }
        swap(arr, l + (int) (Math.random() * (r - l + 1)), r);
        int[] m = partition(arr, l, r);
        // 下面的代码替代了递归
        Stack<StackTmp> stack = new Stack<>();
        stack.push(new StackTmp(l, m[0] -1));
        stack.push(new StackTmp(m[0] + 1, r));

        while (!stack.isEmpty()) {
            StackTmp pop = stack.pop();
            if(pop.l < pop.r) {
                swap(arr, pop.l + (int) (Math.random() * (pop.r - pop.l + 1)), pop.r);
                int[] range = partition(arr, pop.l, pop.r);
                stack.push(new StackTmp(pop.l, range[0] - 1));
                stack.push(new StackTmp(range[1] + 1, pop.r));
            }
        }
    }

六、归并排序

归并排序其实就是一种递归合并排序的意思，实际上是一种分而治之的一种思想，将数组分为左半部分和右半部分，先将左边和右边排好序之后在合并在一起。合并的时候用先用左边的第一个元素和右边的每个元素对比，那个小就放在辅助数组里面。之后将左边或右边剩余的元素移到辅助数组里面即可。

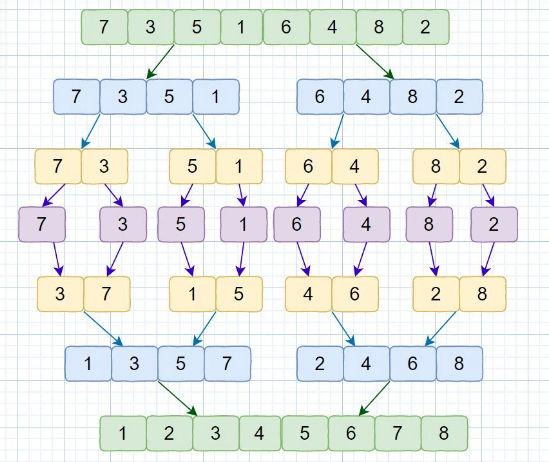
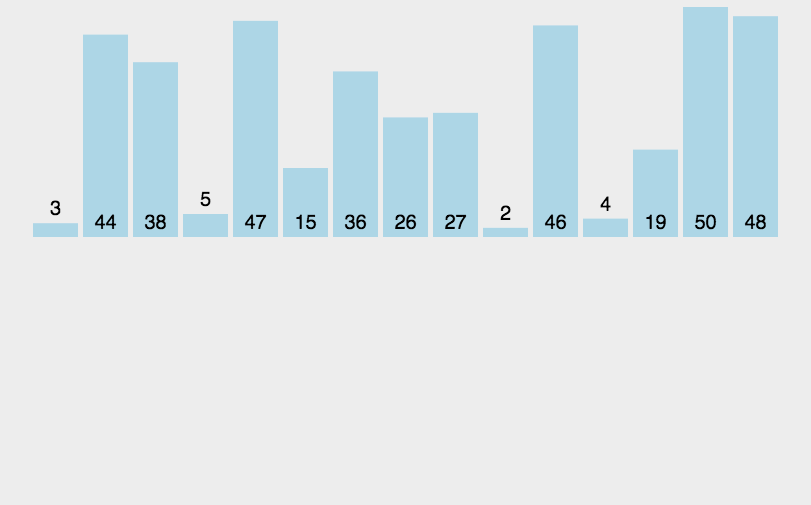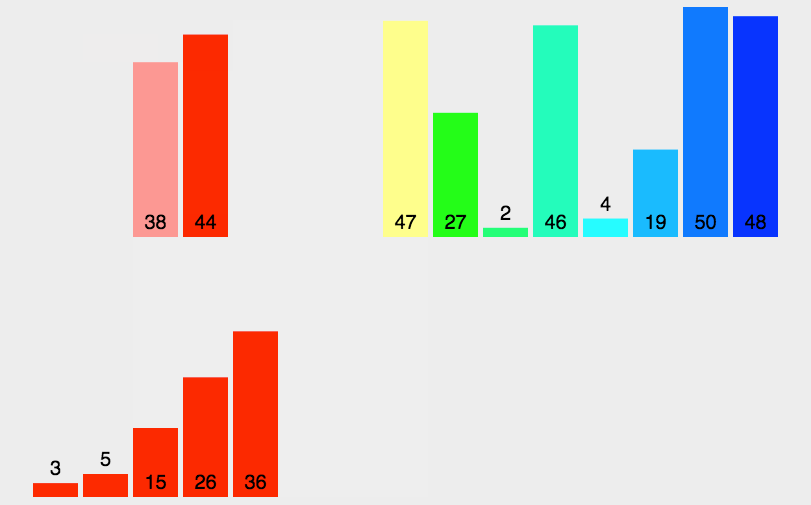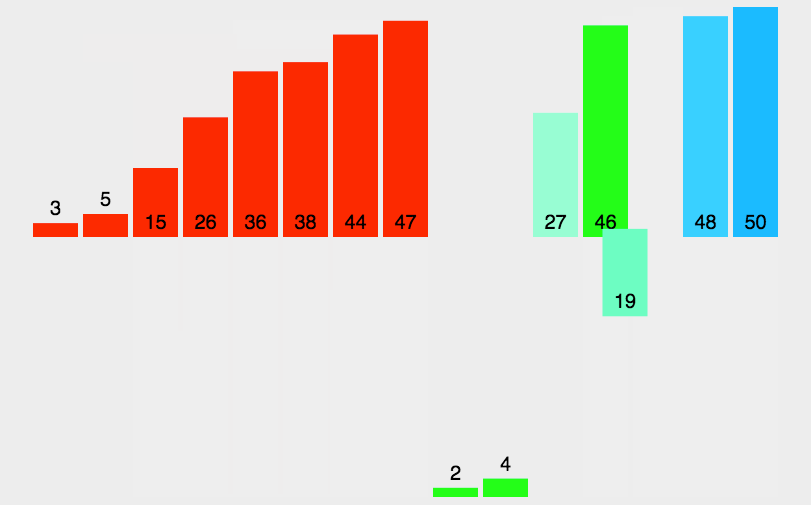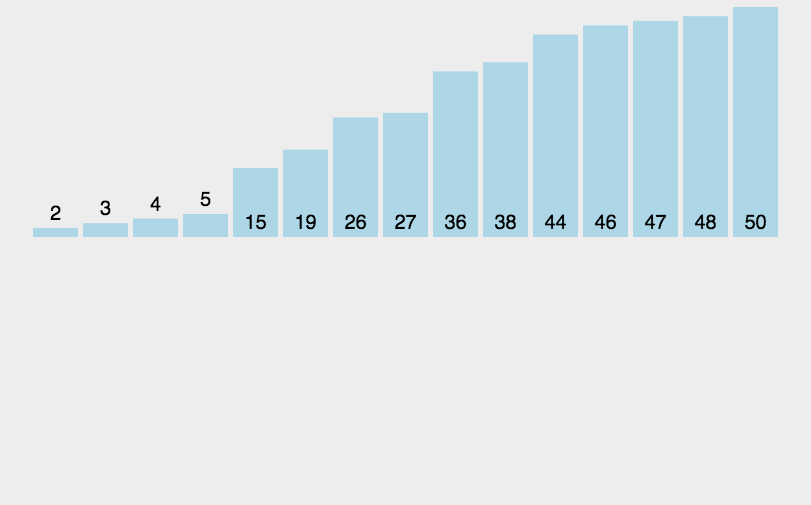
1、归并排序代码实现

    public static void sort(int[] arr) {
        if(arr == null || arr.length < 2) {
            return;
        }
        process(arr, 0, arr.length -1);
    }

    private static void process(int[] arr, int left, int right) {
        if(left == right) {
            return;
        }
        // 获取数组中间值
        int middle = left + (right - left) / 2;
        // 先排左边的
        process(arr, left, middle);
        // 在排右边的
        process(arr, middle + 1, right);
        // 之后合并两边的值
        merge(arr, left, middle, right);
    }

    private static void merge(int[] arr, int left, int middle, int right) {
        // 利用辅助数组实现
        int[] help = new int[right - left + 1];
        // 辅助数组下标
        int index = 0;

        // 左边第一个下标
        int leftIndex = left;
        // 右边第一个下标
        int rightIndex = middle + 1;

        // 用左边的值和右边的所有数对比，如果谁小谁放在help里面
        while (leftIndex <= middle && rightIndex <= right) {
            help[index++] = arr[leftIndex] <= arr[rightIndex] ? arr[leftIndex++] : arr[rightIndex++];
        }

        // 左边｜右边 还有数没有比较的则直接将数据放入help
        while (leftIndex <= middle) {
            help[index++] = arr[leftIndex++];
        }
        while (rightIndex <= right) {
            help[index++] = arr[rightIndex++];
        }

        // 将辅助的数据（已排好序） 替换到原数组里面
        for (int i = 0; i < help.length; i++) {
            arr[left + i] = help[i];
        }
    }

2、小和: 数组中一个数左边比它小的数的总和

小和计算逻辑

public static int count(int[] arr) {
        int ans = 0;
        for (int i = 0; i < arr.length; i++) {
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[i] > arr[j]) {
                    ans++;
                }
            }
        }
        return ans;
    }

归并排序实现

    // 排序
    public static int sort(int[] arr) {
        if(arr == null || arr.length < 2) {
            return 0;
        }
        return process(arr, 0, arr.length - 1);
    }
    
    // 给定数组的指定l～r排序
    private static int process(int[] arr, int l, int r){
        if(l == r) {
            return 0;
        }
        int m = l + (r - l) / 2;
        return process(arr, l, m) + process(arr, m + 1, r) + merge(arr, l, m, r);
    }

    // 合并排序
    private static int merge(int[] arr, int l, int m, int r) {
        int[] help = new int[r - l + 1];
        int p1 = l,p2 = m + 1,index = 0,res = 0;
        while (p1 <= m && p2 <= r) {
            // 如果左边的小于右边的，则小合等于(r - p2 +1) * arr[p1]
            res += arr[p1] < arr[p2] ? (r - p2 +1) * arr[p1] : 0;
            help[index++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
        }

        while (p1 <= m) {
            help[index++] = arr[p1++];
        }
        while (p2 <= r) {
            help[index++] = arr[p2++];
        }

        for (int i = 0; i < help.length; i++) {
            arr[l + i] = help[i];
        }
        return res;
    }

3、逆序对:返回数组中所有的逆序对数量

任何一个前面的数a和任何一个后面的数b都是降序

逆序对逻辑

    public static int count(int[] arr) {
        int ans = 0;
        for (int i = 0; i < arr.length; i++) {
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[i] > arr[j]) {
                    ans++;
                }
            }
        }
        return ans;
    }

归并排序实现

    // 归并排序方式的逆序对计算
   public static int sort(int[] arr) {
        if(arr == null || arr.length < 2) {
            return 0;
        }
        return process(arr, 0, arr.length-1);
    }

    public static int process(int[] arr, int l, int r){
        if(l == r) {
            return 0;
        }
        int m = l + (r - l) / 2;
        return process(arr, l, m) + process(arr, m + 1, r) + merge(arr, l, m, r);
    }

    public static int merge(int[] arr, int l, int m, int r) {
        int[] help = new int[r - l + 1];
        int i = help.length - 1;
        int p1 = m;
        int p2 = r;
        int res = 0;
        while (p1 >= l && p2 > m) {
            // 和归并排序不同的地方
            res += arr[p1] > arr[p2] ? p2 - m : 0;
            help[i--] = arr[p1] > arr[p2] ? arr[p1--] : arr[p2--];
        }
        while (p1 >= l) {
            help[i--] = arr[p1--];
        }
        while (p2 > m) {
            help[i--] = arr[p2--];
        }

        for (int i1 = 0; i1 < help.length; i1++) {
            arr[l + i1] = help[i1];
        }
        return res;
    }

4、数组中的每个数num存在多少个*2<num

普通代码实现逻辑

	public static int count(int[] arr) {
		int ans = 0;
		for (int i = 0; i < arr.length; i++) {
			for (int j = i + 1; j < arr.length; j++) {
				if (arr[i] > (arr[j] << 1)) {
					ans++;
				}
			}
		}
		return ans;
	}

归并排序实现

    public static int sort(int[] arr) {
        if(arr == null || arr.length < 2) {
            return 0;
        }
        return process(arr, 0, arr.length - 1);
    }

    private static int process(int[] arr, int l, int r){
        if(l == r) {
            return 0;
        }
        int m = l + ((r - l) >> 1);
        return process(arr, l, m) + process(arr, m + 1, r) + marge(arr, l, m, r);
    }

    private static int marge(int[] arr, int l, int m, int r) {
        // 遍历左边的值，用左边的值和右边的值进行比较.
        // 将比较的逻辑抽离出来，放在下面的辅助数组逻辑里面逻辑会复杂很多。 这里最主要的优势是不回退
        int res = 0;
        int rightIndex = m + 1;
        for (int i = l; i <= m; i++) {
            // 数组从左往右递增，rightIndex值的2倍小于等于i的值时结束
            while (rightIndex <= r && (long)arr[i] > (long)(arr[rightIndex] * 2L)) {
                rightIndex++;
            }
            res += rightIndex - m -1;
        }
        
        // 归并排序的逻辑
        int[] help = new int[r - l + 1];
        int i = 0;
        int lIndex = l;
        int rIndex = m + 1;
        while (lIndex <= m && rIndex <= r) {
            // 那个小于就先将值放入help
            help[i++] = arr[lIndex] <= arr[rIndex] ? arr[lIndex++] : arr[rIndex++];
        }

        while (lIndex <= m) {
            help[i++] = arr[lIndex++];
        }
        while (rIndex <= r) {
            help[i++] = arr[rIndex++];
        }
        for (int j = 0; j < help.length; j++) {
            arr[l + j] = help[j];
        }
        return res;
    }

5、给定数组有多少组在指定的lower～upper范围上

https://leetcode.com/problems/count-of-range-sum/

前缀累加和：利用一个辅助数组遍历一次存储累加和，后面使用的时候直接通过下标取值。

   public static int countRangeSum(int[] arr, int lower, int upper) {
        if(arr == null || arr.length ==0) {
            return 0;
        }

        // 1、用辅助数组记录所有的位置上面的累加和
        long[] sum = new long[arr.length];
        sum[0] = arr[0];
        for (int i = 1; i < arr.length; i++) {
            sum[i] = sum[i-1] + arr[i];
        }

        return process(sum, 0, sum.length - 1, lower, upper);
    }

    private static int process(long[] arr, int l, int r, int lower, int upper){
        if(r == l) {
            // 2、直接判断值是否在lower～upper上面
            return arr[l] >= lower && arr[r] <= upper ? 1 : 0;
        }

        int m = l + ((r - l) >> 1);
        return process(arr, l, m, lower, upper) + process(arr, m + 1, r, lower, upper) + merge(arr, l, m, r, lower, upper);
    }

    private static int merge(long[] arr, int l, int m, int r, int lower, int upper) {
        // 3、用两个下标记录在这个范围上的值就在lower～upper上面
        int windowL = l;
        int windowR = l;
        // 已知：arr[i~j]在lower~upper里面则arr[0~j] - arr[0~(i-1)]，  [0~j]的整体累加和是x
        // 求arr[0~i]中的前缀和在lower~upper上面 等同于 有多个前缀和在[(x-upper) ~ (x-lower)]上
        int res = 0;
        for (int i = m + 1; i <= r; i++) {
            long min = arr[i] - upper;
            long max = arr[i] - lower;
            while (windowL <= m && arr[windowL] < min) {
                windowL++;
            }
            while (windowR <= m && arr[windowR] <= max) {
                windowR++;
            }
            res += windowR - windowL;
        }

        // 4、归并排序逻辑
        long[] help = new long[r - l + 1];
        int left = l;
        int right = m + 1;
        int i = 0;
        while (left <= m && right <= r) {
            help[i++] = arr[left] <= arr[right] ? arr[left++] : arr[right++];
        }

        // 剩余数字直接赋值
        while (left <= m) {
            help[i++] = arr[left++];
        }
        while (right <= r) {
            help[i++] = arr[right++];
        }

        // 将help里面的数字和arr里面的进行替换
        for (int i1 = 0; i1 < help.length; i1++) {
            arr[l + i1] = help[i1];
        }
        return res;
    }

七、堆-无稳定性

堆就是一颗完全二叉树：一个节点可以算完全二叉树、从左往右的二叉树都是完全二叉树， 先右后左的就不是二叉树。

A video

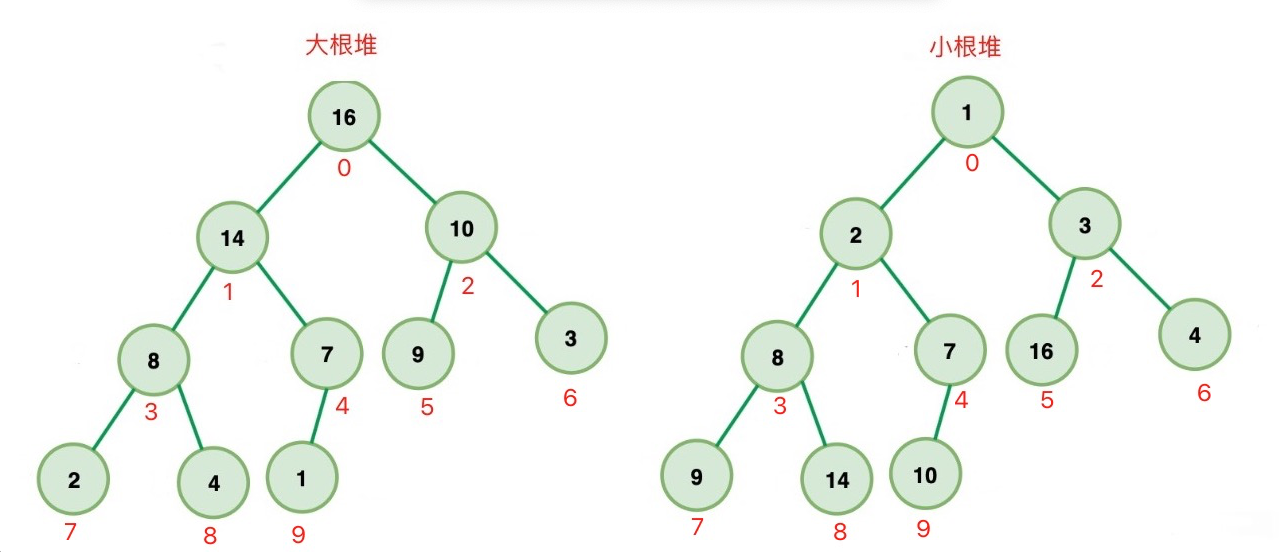
堆规律总结：

节点的父位置：(i - 1) / 2
节点的左孩子：2 * i + 1
节点的右孩子：2 * i + 2

在实现堆的时候一般构建两个函数，一个是push另一个是pop。push实现的时候主要就是通过上浮的方式实现，将新的值放在堆的最后后面，然后对比大小进行上浮操作（谁大谁往前）。pop操作将第一个记录下来用于返回，之后将第一个值和最后一个值进行交换，然后将替换后的第一个值进行下沉操作即可。连续下沉就是排序的操作。

// 堆的代码实现
class MaxHeap{

        public int[] heap;

        public int heapSize;

        public int limit;

        public MaxHeap(int limit) {
            this.heap = new int[limit];
            this.limit = limit;
            this.heapSize = 0;
        }

        public void push(int val) {
            if(heapSize == limit) {
                System.out.println("堆满了");
                return;
            }
            this.heap[this.heapSize] = val;
            insertHeap(this.heap, this.heapSize++);
        }

        public int pop() {
            int root = heap[0];
            swap(heap, 0, --heapSize);
            sink(this.heap, 0);
            return root;
        }


        private void sink(int[] heap, int index) {
            int left = index * 2 + 1;
            while (left < this.heapSize) {
                // 获取index，index的左孩子，index的右孩子中最大的一个下标
                int max = left + 1 < this.heapSize && heap[left + 1] > heap[left] ? left + 1 : left;
                max = heap[index] > heap[max] ? index : max;
                
                // 当前值就是最大的则跳出循环
                if(max == index) {
                    break;
                }

                swap(heap, index, max);
                index = max;
                left = index * 2 + 1;
            }
        }

        // 将最后一个节点的位置按照大根堆的方式合适的位置，上移
        private void insertHeap(int[] heap, int index){
            // (index-1)/2 就是 index节点的父节点
            while (heap[index] > heap[(index-1)/2]) {
                swap(heap, index, (index-1)/2);
                index = (index-1)/2;
            }
        }
    }

1、堆排序

堆排序是通过将数组堆化，之后在将第一个数字放到最后然后逐个下沉来完成排序。堆化的方式有两种，一种是上浮O(N*logN)，一种是下沉O(N)

public static class MaxHeap{

        private int[] heap;

        private int heapSize;

        // 方式一：通过上浮的方式组装大根堆O(N*logN)
        public void sortMax(int[] arr) {
            for (int i = 0; i < arr.length; i++) {
                ascendHeap(arr, i);
            }

            int heapSize = arr.length;
            swap(arr, 0, --heapSize);
            while (heapSize > 0) {
                sink(arr, 0, heapSize);
                swap(arr, 0, --heapSize);
            }
        }

        //方式二： 通过下沉的方式组装大根堆O(N)
        public void sortSink(int[] arr) {
            for(int i = arr.length - 1; i >= 0; i--) {
                sink(arr, i, arr.length);
            }

            int heapSize = arr.length;
            swap(arr, 0, --heapSize);
            while (heapSize > 0) {
                sink(arr, 0, heapSize);
                swap(arr, 0, --heapSize);
            }
        }

        // 上浮
        private void ascendHeap(int[] heap, int index) {
            while (heap[index] > heap[(index-1)/2]){
                swap(heap, index, (index-1)/2);
                index = (index-1)/2;
            }
        }

        // 下沉
        private void sink(int[] heap, int index, int heapSize) {
            // 将第一个下沉
            int left = index * 2 + 1;
            while (left < heapSize) {
                // 获取index、left、right中最大的下标
                int largest = left + 1 < heapSize && heap[left + 1] > heap[left] ? left + 1 : left;
                largest = heap[index] > heap[largest] ? index : largest;
                if(index == largest) {
                    break;
                }
                swap(heap, index, largest);
                left = (largest * 2) + 1;
                index = largest;
            }
        }
    }

2、题目

2.1、移动指导长度的排序最优排序

给定一个数组，已知单个元素排序需要移动的最大长度是k，求一个合适的排序规则。

   // 先将指定k长度的值放到队列里面，之后同步将其他的值放到队列里面并poll值到数组里面（数组移动最大长度为k） 
   public static void sort(int[] arr, int k) {
        if(arr == null || k == 0) {
            return;
        }
        PriorityQueue<Integer> queue = new PriorityQueue<Integer>();
        int index = 0;
        // 将k-1里面的值放在队列里面
        for (index = 0; index < Math.min(arr.length - 1, k - 1); index++) {
            queue.add(arr[index]);
        }

        // 将index后面的值也放到队列里面，同时将小根堆里面的数据依次替换到数组里面
        for (int i = 0; i < arr.length; i++, index++) {
            if(index < arr.length) {
                queue.add(arr[index]);
            }
            arr[i] = queue.poll();
        }
    }

2.2、最大线段重合问题

题目：给定很多线段start~end,求最多重合区域值 1、线段左右都是闭区间，一定都是整数 2、重合区长度必须>=1

    /**
     * 1、先将线段的开始位置从小到大排序
     * 2、利用小根堆，将小根堆中的最小值 小于等于 当前线段start的值弹出
     * 3、将线段的end值放入大根堆中
     */
    public static int maxLineSegmentSum(int[][] arr) {
        Arrays.sort(arr, (a, b) -> a[0] - b[0]);

        PriorityQueue<Integer> queue = new PriorityQueue<>();
        int max = 0;
        for (int[] ints : arr) {
            if(!queue.isEmpty() && queue.peek() <= ints[0]) {
                queue.poll();
            }
            queue.add(ints[1]);
            max = Math.max(max, queue.size());
        }
        return max;
    }

2.3、加强堆

利用hashMap实现

public class HeapGreater<T> {
    // 堆
    private ArrayList<T> heap;

    // 利用hashMap存储下标
    private HashMap<T, Integer> hashMap;

    private int headSize;

    private Comparator<T> comparator;

    public HeapGreater(Comparator<T> comparator) {
        this.comparator = comparator;
        this.heap = new ArrayList<>();
        this.headSize = 0;
        this.hashMap = new HashMap<>();
    }

    public void push(T obj) {
        heap.add(obj);
        hashMap.put(obj, headSize);
        ascend(headSize++);
    }

    public T pop() {
        T t = heap.get(0);
        swap(heap, 0, --headSize);
        sink(0);
        hashMap.remove(t);
        heap.remove(headSize);
        return t;
    }

    public int size() {
        return headSize;
    }

    public void remove(T obj) {
        // 将最后一个值拿出来
        T val = heap.get(headSize - 1);
        int index = hashMap.get(obj);
        heap.remove(--headSize);
        hashMap.remove(obj);
        if(comparator.compare(val, obj) != 0) {
            heap.set(index, val);
            hashMap.put(val, index);
            adjust(val);
        }
    }

    // 调整位置，向上浮后往下沉
    public void adjust(T obj) {
        ascend(hashMap.get(obj));
        sink(hashMap.get(obj));
    }

    // 下沉
    private void sink(int index) {
        int left = index * 2 + 1;
        while (left < headSize) {
            int max = left + 1 < headSize && comparator.compare(heap.get(left), heap.get(left + 1)) > 0 ? left + 1 : left;
            max = comparator.compare(heap.get(max), heap.get(index)) < 0 ? max : index;
            if(index == max) {
                break;
            }
            swap(heap, index, max);
            index = max;
            left = (max * 2) + 1;
        }
    }

    // 上浮
    private void ascend(int index) {
        while (comparator.compare(heap.get(index), heap.get((index - 1) / 2)) < 0) {
            swap(heap, index, (index - 1) / 2);
            index = (index - 1) / 2;
        }
    }
    
    private void swap(ArrayList<T> arr, int i, int j) {
        if(i == j) {
            return;
        }
        T tmp = arr.get(i);
        T jTmp = arr.get(j);
        arr.set(i, jTmp);
        arr.set(j, tmp);
        hashMap.put(tmp, j);
        hashMap.put(jTmp, i);
    }
}

3、前缀树

将字符串数组按照字符组装为一颗树，便于查找字符的前缀出现了多少次。实现方式有两种，一种是通过数组另外一种就是通过hash表，两种实现的方式都是一样的只是容器不一样。

3.1、数组实现前缀树

public static class Tire{

        public Node root;

        public Tire() {
            this.root = new Node();
        }

        // 插入字符串
        public void insert(String str) {
            if(str == null || str.isEmpty()) {
                return;
            }

            char[] chars = str.toCharArray();
            Node node = root;
            for (int i = 0; i < chars.length; i++) {
                int index = chars[i] - 'a';
                if(node.nexts[index] == null) {
                    node.nexts[index] = new Node();
                }
                node = node.nexts[index];
                node.pass++;
            }
            node.end++;
        }

        // 删除字符串
        public void del(String str) {
            if(str == null || str.isEmpty() || findCount(str) == 0) {
                return;
            }
            char[] chars = str.toCharArray();
            Node node = root;
            node.pass--;
            for (int i = 0; i < chars.length; i++) {
                int index = chars[i] - 'a';
                if(--node.nexts[index].pass == 0) {
                    node.nexts[index] = null;
                    return;
                }
                node = node.nexts[index];
            }
            node.end--;
        }

        // 获取字符串出现了几次
        public int findCount(String str) {
            if(str == null || str.isEmpty()) {
                return 0;
            }
            char[] chars = str.toCharArray();
            Node node = root;
            for (int i = 0; i < chars.length; i++) {
                int index = chars[i] - 'a';
                if(node.nexts[index] == null) {
                    return 0;
                }
                node = node.nexts[index];
            }
            return node.end;
        }

        // 获取有多少个符合str的前缀字符串
        public int prefixCount(String str) {
            if(str == null || str.isEmpty()) {
                return 0;
            }
            char[] chars = str.toCharArray();
            Node node = root;
            for (int i = 0; i < chars.length; i++) {
                int index = chars[i] - 'a';
                if(node.nexts[index] == null) {
                    return 0;
                }
                node = node.nexts[index];
            }
            return node.pass;
        }
    }

    public static class Node{

        public int pass;

        public int end;

        public Node[] nexts;

        public Node() {
            this.pass = 0;
            this.end = 0;
            // 按照26个字母作为路径
            this.nexts = new Node[26];
        }
    }

3.2、Hash表实现前缀树

class PrefixTree{

    private Node root;

    public T002PrefixTreeHash() {
        this.root = new Node();
    }

    public void insert(String str) {
        if(str == null || str.isEmpty()) {
            return;
        }
        char[] chars = str.toCharArray();
        Node node = root;
        for (int i = 0; i < chars.length; i++) {
            int index = chars[i];
            if(!node.hashMap.containsKey(index)){
                node.hashMap.put(index, new Node());
            }
            node.hashMap.get(index).pass++;
            node = node.hashMap.get(index);
        }
        node.end++;
    }

    public void del(String str){
        if(findCount(str) == 0) {
            return;
        }

        if(str == null || str.isEmpty()) {
            return;
        }
        char[] chars = str.toCharArray();
        Node node = root;
        for (int i = 0; i < chars.length; i++) {
            int index = chars[i];
            if(--node.hashMap.get(index).pass == 0) {
                node.hashMap.remove(index);
                return;
            }
            node = node.hashMap.get(index);
        }
        node.end--;
    }

    public int findCount(String str) {
        if(str == null || str.isEmpty()) {
            return 0;
        }
        char[] chars = str.toCharArray();
        Node node = root;
        for (int i = 0; i < chars.length; i++) {
            int index = chars[i];
            if(node.hashMap.get(index) == null){
                return 0;
            }
            node = node.hashMap.get(index);
        }
        return node.end;
    }

    public int prefixCount(String str) {
        if(str == null || str.isEmpty()) {
            return 0;
        }
        char[] chars = str.toCharArray();
        Node node = root;
        for (int i = 0; i < chars.length; i++) {
            int index = chars[i];
            if(node.hashMap.get(index) == null) {
                return 0;
            }
            node = node.hashMap.get(index);
        }
        return node.pass;
    }

    public static class Node{

        public int pass;

        public int end;

        public HashMap<Integer, Node> hashMap;

        public Node() {
            this.pass = 0;
            this.end = 0;
            this.hashMap = new HashMap<>();
        }

    }
}

八、计数排序

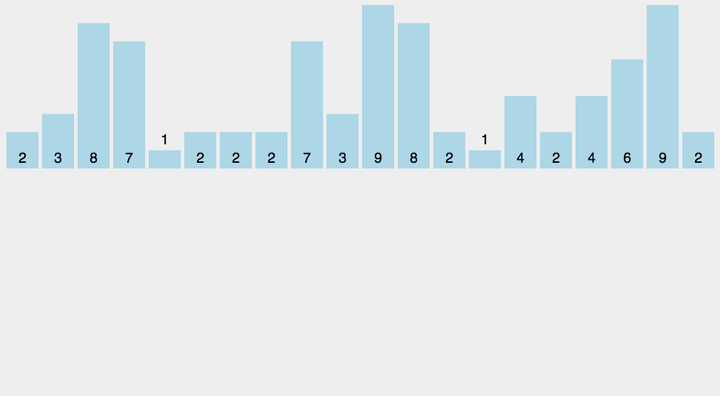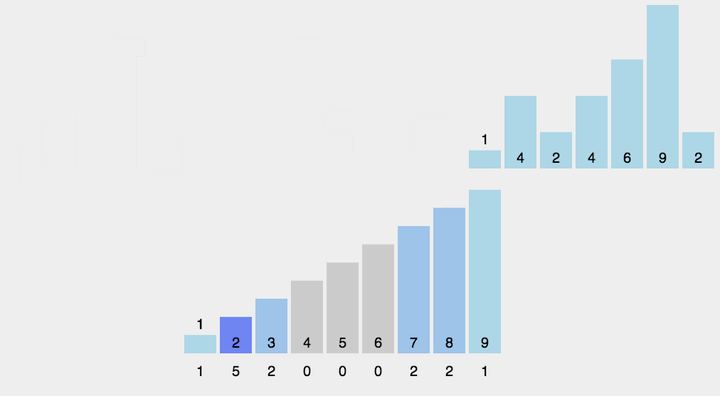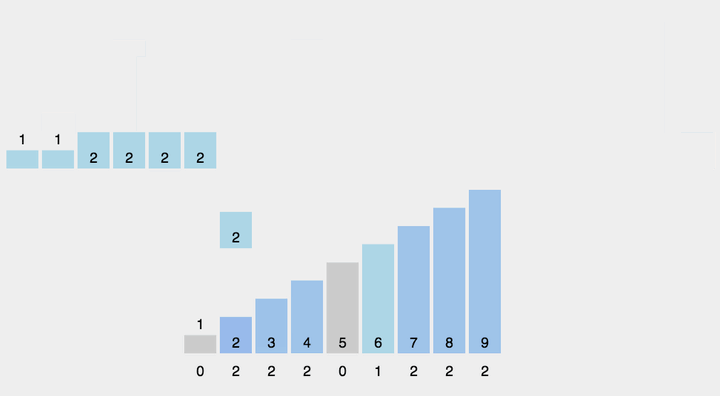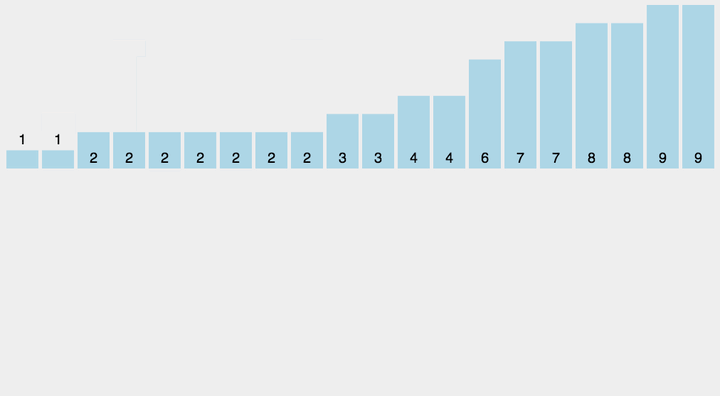
基数排序的是基于桶的思想，有局限性。如果数据量差距特别大的情况下（重复数少比如1～1w的连续数字排序），桶就需要特别多这种情况就不适合使用基数排序。只有数据的重复值比较多比如班级的年龄排序时候使用基数排序就比较合适。

  // 分为三步：1、计算出数组中最大的值。2、用最大的值创建桶，将数组中的值出现次数放入桶中，桶的下标就是数组的元素。3、将桶中的数据获取值后替换到原数组中
  public static void sort(int[] arr) {
        if(arr == null || arr.length < 2) {
            return;
        }
        int max = 0;
        for (int j : arr) {
            max = Math.max(max, j);
        }

        int[] bucket = new int[max + 1];
        for (int i : arr) {
            bucket[i]++;
        }

        int j = 0;
        for (int i = 0; i < bucket.length; i++) {
            int count = bucket[i];
            if(count < 1) {
                continue;
            }
            while (count > 0) {
                arr[j++] = i;
                count--;
            }
        }
    }

九、基数排序

如将3位数进行排序，就先将个位排好序，之后将十位排序，最后将百位排好序就完成了整个数字的排序。在排个位时候，先准备一个0～9的桶，然后依次将个位对应的元素放入桶中，然后依次取出，之后按照个位进行十位和百位的排序。

   // 初始化的数组默认值是0，利用0判断数组里面是否存在数字
    public static void sort(int[] arr) {
        // 获取最大值的位置
        int digit = getMaxDigit(arr);
        // 遍历所有的位数
        for(int j = 1; j <= digit; j++) {
            // 将j位置的数据按照下标放在指定桶中
            int[][] help = new int[10][10];
            for (int i = 0; i < arr.length; i++) {
                int val = getElement(arr[i], j);
                int[] ints = help[val];
                for (int i1 = 0; i1 < ints.length; i1++) {
                    if(ints[i1] == 0) {
                        ints[i1] = arr[i];
                        break;
                    }
                }
            }
            // 将桶中的数字依次取出放回原来的数字
            int index = 0;
            for (int i = 0; i < help.length; i++) {
                int[] ints = help[i];
                if (ints != null && ints.length > 0) {
                    for (int d = 0; d < ints.length; d++) {

                        if(ints[d] == 0) {
                            break;
                        }
                        arr[index] = ints[d];
                        index++;
                    }
                }
            }
        }
    }

    // 利用数组的最后一个数字存储数量, 但是不支持负数，需要支持负数的话。可以将所有数乘以指定数后变为正数，排序完成后在调整为负数
    public static void sort1(int[] arr) {
        // 获取最大值的位置
        int digit = getMaxDigit(arr);

        // 遍历所有的位数
        for(int j = 1; j <= digit; j++) {
            // 将j位置的数据按照下标放在指定桶中
            int[][] help = new int[10][11];
            for (int i = 0; i < arr.length; i++) {
                int val = getElement(arr[i], j);
                int[] ints = help[val];
                int index = ints[10]++;
                ints[index] = arr[i];
            }
            // 将桶中的数字依次取出放回原来的数字
            int index = 0;
            for (int i = 0; i < help.length; i++) {
                int[] ints = help[i];
                if (ints[10] == 0) {
                    continue;
                }
                for (int d = 0; d < ints[10]; d++) {
                    arr[index++] = ints[d];
                }
            }
        }
    }



    // 最优的方式，将二维数组的桶换成了数组。 利用累加和的方式进行基数排序
    public static void sort2(int[] arr) {
       int[] help = new int[arr.length];
        // 获取最大值的位置
        int digit = getMaxDigit(arr);
        for (int i = 1; i <= digit; i++) {
            int[] bucket = new int[10];
            // 将数组i位置的数据出现次数放入桶中
            for (int j = 0; j < arr.length; j++) {
                int index = getElement(arr[j], i);
                bucket[index]++;
            }
            // 将桶变为累加和（累加和的值就是数字出现的次数）
            for (int j = 1; j < bucket.length; j++) {
                bucket[j] = bucket[j] + bucket[j -1];
            }
            // 通过桶中的累加将数组的中的元素按序放入help
            for (int j = arr.length - 1; j >= 0; j--) {
                int index = getElement(arr[j], i);
                // 重点：从右往左获取数组的元素，元素值的位置就是元素出现的次数减一（bucket[index] - 1）
                help[bucket[index] - 1] = arr[j];
                bucket[index]--;
            }
            // 将help数据替换到数组中
            for (int j = 0; j < help.length; j++) {
                arr[j] = help[j];
            }
        }
    }

    // 获取最大值的位数
    private static int getMaxDigit(int[] arr) {
        int max = 0;
        for (int i : arr) {
            max = Math.max(max, i);
        }
        int digit = 0;
        while (max != 0) {
            digit++;
            max /= 10;
        }
        return digit;
    }
    
    // 获取数组第几位上面的数字
    public static int getElement(int val, int i) {
        String str = String.valueOf(val);
        char[] chars = str.toCharArray();
        if(chars.length < i) {
            return 0;
        }
        return Integer.parseInt(String.valueOf(chars[chars.length - i]));
    }

十、总结

算法名称	实现方式	时间复杂度	额外空间复杂度	稳定性
1选择排序(比较)	每次找到最小的值进行替换	O(N^2)	O(1)	无
2冒泡排序(比较)	两两比较小前大后	O(N^2)	O(1)	有
3插入排序(比较)	从后面取出一个数插入到前面已经排序好的元素里面	O(N^2)	O(1)	有
4希尔排序(比较)	将数组分为若干个数组有进行插入排序	O(N^(1.3-2))	O(1)	无
5快速排序(比较)	荷兰国旗方式进行排序	O(N*logN)	O(logN)	无
6归并排序(比较)	递归合并排序，将数组从中间分开依次进行排序	O(N*logN)	O(N)	有
7堆排序(比较)	将数组元素组装为堆结构后排序	O(N*logN)	O(1)	无
8计数排序(桶)	找出数据的最大值创建一个桶，将数字放入桶中依次取出	O(N)	O(M)	有
9基数排序(桶)	将元素按照位数拆分，依次从个位开始排序所有位置排完后取出	O(N)	O(N)	有

1、不基于比较的排序，对数据样本有限制不易改写

2、基于比较的排序时间复杂度的极限是O(N*logN)

3、时间复杂度O(N*logN)、额外空间复杂度低于O(N)、且稳定的排序目前没有

4、只要求速度的选快排、空间最小的是堆排序、稳定的选归并排序

十一、引用

1、算法图https://www.runoob.com/w3cnote/ten-sorting-algorithm.html

2、算法题目https://www.mashibing.com/