04_二叉树学习

About 14 minstudyalgorithm

一、链表递归实现先序、中序、后序

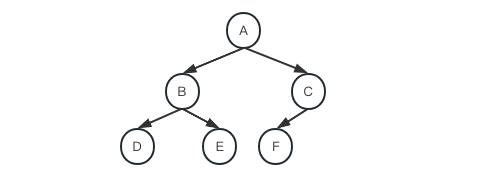
遍历的先序中序后序是按照头节点在前面、中间、后面区分的。分别为：
先序：头、左、右，上图遍历顺序ABDECF
中序：左、头、右，上图遍历顺序DBEAFC
后序：左、右、头，上图遍历顺序DEBFCA

	// 先序打印所有节点
	public static void pre(Node head) {
		if (head == null) {
			return;
		}
		System.out.println(head.value);
		pre(head.left);
		pre(head.right);
	}

	public static void in(Node head) {
		if (head == null) {
			return;
		}
		in(head.left);
		System.out.println(head.value);
		in(head.right);
	}

	public static void pos(Node head) {
		if (head == null) {
			return;
		}
		pos(head.left);
		pos(head.right);
		System.out.println(head.value);
	}

二、链表非递归实现先序、中序、后序

先序

1、利用栈实现将头、右、左(元素不为空)依次push到栈中

2、循环弹出的值就是先序

    // 先序遍历打印
    public static void pre(Node node) {
        if(node == null) {
            return;
        }
        Stack<Node> stack = new Stack<>();
        stack.add(node);
        while (!stack.isEmpty()) {
            Node pop = stack.pop();
            System.out.print(pop.val);

            if(pop.right != null) {
                stack.push(pop.right);
            }

            if(pop.left != null) {
                stack.push(pop.left);
            }
        }
    }

中序

1、先将所有的左子节点入栈，到null为止

2、从栈中弹出节点，并将弹出节点的右子节点作为头重复步骤1. 弹出的节点就是中序

3、栈为空停止遍历

    // 中序遍历打印
    public static void in(Node node) {
        if(node == null) {
            return;
        }
        Stack<Node> stack = new Stack<>();
        while (!stack.isEmpty() || node != null) {
            if(node != null) {
                stack.push(node);
                node = node.left;
            } else {
                node = stack.pop();
                System.out.print(node.val);
                node = node.right;
            }
        }
    }

后序

1、利用栈实现先左后右(元素不为空)的push到栈中

2、循环加入到另外一个栈中

3、循环弹出第二个栈的值就是后序

    // 后序遍历打印(和先序不同的就是先左在右，之后逆序输出即可)
    public static void pos(Node node) {
        if(node == null) {
            return;
        }
        Stack<Node> stack = new Stack<>();
        Stack<Node> pos = new Stack<>();

        stack.add(node);
        while (!stack.isEmpty()) {
            Node pop = stack.pop();
            pos.push(pop);
            if(pop.left != null) {
                stack.push(pop.left);
            }
            if(pop.right != null) {
                stack.push(pop.right);
            }
        }

        while (!pos.isEmpty()) {
            Node pop = pos.pop();
            System.out.print(pop.val);
        }
    }

不用两个栈的方式实现后序，极客写法

三、二叉树按层遍历

按层遍历后: ABCDEF

1、利用队列(先进先出)，将二叉树数据add到队列中，并遍历队列到队列为空为止

2、二叉树的左边存在数据就先放左边的值

    // 按层遍历
    public static void level(Node node) {
        if(node == null) {
            return;
        }
        Queue<Node> queue = new LinkedList<>();
        queue.add(node);

        while (!queue.isEmpty()) {
            // 弹出队列里面的值打印
            Node poll = queue.poll();
            System.out.print(poll.val);

            // 队列里面的存在left｜right则放入队列中
            if(poll.left != null) {
                queue.add(poll.left);
            }

            if(poll.right != null) {
                queue.add(poll.right);
            }
        }
    }

四、二叉树的序列化和反序列化

将二叉树按照节点转换成字符串，不忽视空节点。以及通过字符串转换成二叉树。

先序序列

利用先序遍历的方式序列化

    // 先序序列化
    public static Queue<String> preSerialize(Node node) {
        if(node == null) {
            return null;
        }
        Queue<String> queue = new LinkedList<>();
        pre(node, queue);
        return queue;
    }

    private static void pre(Node node, Queue<String> queue) {
        if(node == null) {
            queue.add(null);
            return;
        }
        queue.add(node.val);
        pre(node.left, queue);
        pre(node.right, queue);
    }

    // 先序反序列化
    public static Node preUnSerialize(Queue<String> queue) {
        if(queue == null || queue.isEmpty()) {
            return null;
        }
        return pre(queue);
    }

    private static Node pre(Queue<String> queue) {
        String poll = queue.poll();
        if(poll == null) {
            return null;
        }
        Node node = new Node(poll);
        node.left = pre(queue);
        node.right = pre(queue);
        return node;
    }

后序序列

利用后序遍历的方式序列化

    // 后序序列化
    public static Queue<String> posSerialize(Node node) {
        if(node == null) {
            return null;
        }
        Queue<String> queue = new LinkedList<>();
        pos(node, queue);
        return queue;
    }

    private static void pos(Node node, Queue<String> queue) {
        if(node == null) {
            queue.add(null);
            return;
        }

        pos(node.left, queue);
        pos(node.right, queue);
        queue.add(node.val);
    }

    // 后序反序列化
    public static Node posUnSerialize(Queue<String> queue) {
        if(queue == null || queue.isEmpty()) {
            return null;
        }

        Stack<String> stack = new Stack<>();
        while (!queue.isEmpty()) {
            stack.push(queue.poll());
        }
        return pos(stack);
    }

    public static Node pos(Stack<String> stack) {
        String pop = stack.pop();
        if(pop == null) {
            return null;
        }
        Node node = new Node(pop);
        node.right = pos(stack);
        node.left = pos(stack);
        return node;
    }

按层序列

利用按层遍历的方式序列化

    // 按层序列化
    public static Queue<String> levelSerialize(Node node) {
        Queue<String> res = new LinkedList<>();
        if(node == null) {
            res.add(null);
            return res;
        }

        Queue<Node> queue = new LinkedList<>();
        queue.add(node);
        res.add(node.val);
        while (!queue.isEmpty()) {
            Node poll = queue.poll();
            if(poll.left != null) {
                queue.add(poll.left);
                res.add(poll.left.val);
            } else {
                res.add(null);
            }

            if(poll.right != null) {
                queue.add(poll.right);
                res.add(poll.right.val);
            } else {
                res.add(null);
            }
        }
        return res;
    }

    // 按层反序列化
    public static Node levelUnSerialize(Queue<String> queue){
        if(queue == null || queue.size() < 1) {
            return null;
        }
        Node head = generateNode(queue.poll());
        Queue<Node> nodeQueue = new LinkedList<>();
        if(head != null) {
            nodeQueue.add(head);
        }

        Node node = null;
        while (!nodeQueue.isEmpty()) {
            node = nodeQueue.poll();
            node.left = generateNode(queue.poll());
            node.right = generateNode(queue.poll());
            if(node.left != null) {
                nodeQueue.add(node.left);
            }
            if(node.right != null) {
                nodeQueue.add(node.right);
            }
        }
        return node;
    }

    private static Node generateNode(String val) {
        if(val == null) {
            return null;
        }
        return new Node(val);
    }

五、多叉树和二叉树互转

leetcode 431题 https://leetcode.com/problems/encode-n-ary-tree-to-binary-tree

一颗多叉树转为二叉树(所有的子节点都放在二叉树的左树的右边界上面)，之后将二叉树转为之前的多叉树

// 将多叉数转尾二叉树
    public static TreeNode encode(Node node) {
        if(node == null) {
            return null;
        }
        
        TreeNode treeNode = new TreeNode(node.val);
        treeNode.left = en(node.children);
        return treeNode;
    }
    
    public static TreeNode en(List<Node> nodes) {
        if(nodes == null || nodes.isEmpty()) {
            return null;
        }
        TreeNode head = null, current = null;
        for (Node node : nodes) {
            TreeNode treeNode = new TreeNode(node.val);
            // 记录头节点用于返回
            if(head == null) {
                head = treeNode;
            } else {
                // 将多叉节点一直往右放
                current.right = treeNode;
            }
            current = treeNode;
            // 将子多节点放到左边
            current.left = en(node.children);
        }
        return head;
    }

    // 将二叉树转为多叉树
    public static Node decode(TreeNode treeNode) {
        if(treeNode == null) {
            return null;
        }
        return new Node(treeNode.val, de(treeNode.left));
    }
    
    private static List<Node> de(TreeNode treeNode) {
        if(treeNode == null) {
            return null;
        }
        List<Node> list = new ArrayList<>();
        while (treeNode != null) {
            // 创建节点，children就是所有的左子节点
            Node current = new Node(treeNode.val, de(treeNode.left));
            // 将所有的左节点放到list里面
            list.add(current);
            // 处理下一个节点
            treeNode = treeNode.right;
        }
        return list;
    }

六、设计一个打印整棵树的函数

跳过，可以自行实现

七、求二叉树最宽的层有多少个节点

按层遍历时，记录当前层的结束节点currentEnd, 下一层结束节点nextEnd。

使用Map

public static int maxWidthUseMap(Node head) {
        if(head == null) {
            return 0;
        }
        Queue<Node> queue = new LinkedList<>();
        queue.add(head);

        // 记录所有节点的当前层数
        Map<Node, Integer> map = new HashMap<>();
        map.put(head, 1);
        int currentLevel = 1;
        int levelNumber = 1;
        int max = 0;
        while (!queue.isEmpty()) {
            Node poll = queue.poll();
            // 获取当前节点的层数
            Integer level = map.get(poll);
            if(poll.left != null) {
                queue.add(poll.left);
                map.put(poll.left, level + 1);
            }
            if(poll.right != null) {
                queue.add(poll.right);
                map.put(poll.right, level +1);
            }
            // 如果是同一个层级则增加当前层数数量
            if(level == currentLevel) {
                levelNumber++;
            } 
            // 非同一个层级则遍历到了下一个层级，层级+1和获取最大层级数量
            else {
                currentLevel++;
                max = Math.max(max, levelNumber);
                levelNumber = 1;
            }
        }
        return Math.max(levelNumber, max);
    }

不使用Map

    public static int maxWidth(Node node) {
        if(node == null) {
            return 0;
        }
        Queue<Node> queue = new LinkedList<>();
        queue.add(node);

        int max = 0;
        int currentLevelNumber = 1;

        Node currentRight = node;
        Node nextRight = null;
        while (!queue.isEmpty()) {
            Node poll = queue.poll();
            // 将左右节点放入队列，并赋值最右边的节点
            if(poll.left != null) {
                queue.add(poll.left);
                nextRight = poll.left;
            }

            if(poll.right != null) {
                queue.add(poll.right);
                nextRight = poll.right;
            }
            currentLevelNumber++;
            // 如果弹出的节点是下一个节点的最右节点，则初始化数据后进行下一层数量统计
            if(poll == currentRight) {
                max = Math.max(max, currentLevelNumber);
                currentLevelNumber = 0;
                currentRight = nextRight;
            }

        }
        return max;
    }

八、找到节点的后继节点

在中序遍历中，当前节点x的下一个节点就是后继节点

1、如果x存在右节点，那么x的后继节点就是右节点的最左节点。（右树上的最左）

2、如果x不存在右节点，则x不断往上找父节点，直到找到存在左孩子，则左孩子就是x的后继节点。（当前节点是父节点的左孩子）

public static Node getSuccessorNode(Node node) {
        if(node == null) {
            return node;
        }

        if(node.right != null) {
            Node right = node.right;
            while (right.left != null) {
                right = right.left;
            }
            return right;
        } else {
            Node parent = node.parent;
            // 当前节点是其父节点的右孩子
            while (parent != null && parent.right == node) {
                node = parent;
                parent = parent.parent;
            }
            return parent;
        }
    }

九、二叉树折纸问题

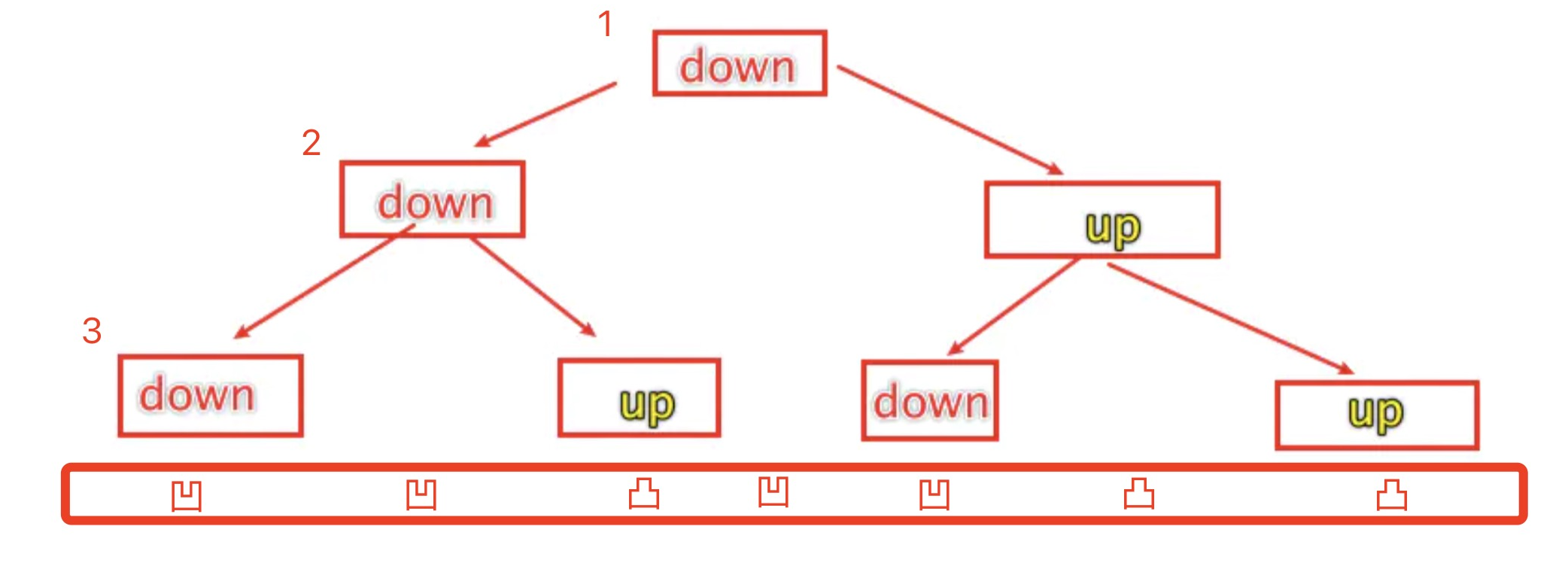
1、头节点是凹的

2、所有左节点是凹，右节点是凸

3、打印按照层数打印就是中序遍历

    public static void paperFolding(int n) {
        process(1, n, true);
    }

    /**
     * true: down
     * false：up
     * i: 当前层数
     * n：所有层数
     * 中序遍历整棵树
     */
    public static void process(int i, int n, boolean down) {
        if(i > n) {
            return;
        }
        process(i + 1, n, true);
        System.out.println(down ? "down" : "up");
        process(i + 1, n, false);
    }

九、判断是否为完全二叉树

1、按层遍历，有右无左则返回false。

2、当第一次遇到没有左右子节点时，剩余节点也必须没有左右子节点

		/**
     * 判断是否为满二叉树，非递归版
     */
    public static boolean isFull(Node node) {
        if(node == null) {
            return false;
        }
        Queue<Node> queue = new LinkedList<>();
        queue.add(node);
        boolean exist = false;
        while (!queue.isEmpty()) {
            Node poll = queue.poll();
            Node l = poll.left;
            Node r = poll.right;
            // 左孩子为空，右孩子不为空则不是
            if(l == null && r != null) {
                return false;
            }

            // 第二次遇到还有null的子节点
            if(exist && (l != null || r != null)) {
                return false;
            }

            if(l != null) {
                queue.add(l);
            }
            if(r != null) {
                queue.add(r);
            }
            // 第一次遇到没有子节点
            if(l == null || r == null) {
                exist = true;
            }
        }
        return true;
    }

十、判断是否为平衡树

所有会出现的情况

1、每一颗子树的左右高度相差的绝对值不超过1

2、左树、右树都必须是平衡二叉树

代码实现

    // 判断是否为平衡二叉树
    public static boolean isBalanced(Node node) {
        return process(node).isBalanced;
    }
    
    public static Info process(Node node) {
        if(node == null) {
            return new Info(true, 0);
        }
        Info l = process(node.left);
        Info r = process(node.right);
        
        // 计算当前层数
        int max = Math.max(l.height, r.height) + 1;

        // 其中一个子节点不是平衡二叉树则当前数不是平衡二叉树
        if(!l.isBalanced || !r.isBalanced) {
            return new Info(false, max);
        }
        // 左右子节点高度相差超过1
        if(Math.abs(l.height - r.height) > 1) {
            return new Info(false, max);
        }
        return new Info(true, max);
    }

十一、判断是否为搜索二叉树

所有会出现的情况

1、头节点左子节点的值都比它小，右子节点的值都比它大

2、左树、右树都必须是搜索二叉树

3、经典二叉树没有重复值

代码实现

方式一：将二叉树用中序遍历，之后判断是否为逆序即可

public static boolean isSearchIn(Node node) {
        if(node == null) {
            return true;
        }
        List<Node> list = new LinkedList<>();
        // 利用中序将数据放到list里面
        in(node, list);
        for (int i = 1; i < list.size(); i++) {
            // 如果存在前面的数大于后面的数则非搜索树
            if(list.get(i).value <= list.get(i -1).value) {
                return false;
            }
        }
        return true;
    }

    public static void in(Node node, List<Node> list) {
        if(node == null) {
            return;
        }
        in(node.left, list);
        list.add(node);
        in(node.right, list);
    }

方式二：利用递归判断

public static boolean isSearch(Node node) {
        if(node == null) {
            return true;
        }
        return process(node).isSearch;
    }

    public static Info process(Node node) {
        if(node == null) {
            return null;
        }
        Info l = process(node.left);
        Info r = process(node.right);

        // 获取左右孩子的最大最小值
        int max = node.value;
        int min = node.value;
        if(l != null) {
            max = Math.max(max, l.max);
            min = Math.min(min, l.min);
        }
        if(r != null) {
            max = Math.max(max, r.max);
            min = Math.min(min, r.min);
        }

        // 左右孩子其中一个非搜索
        if((l != null && !l.isSearch) || (r != null && !r.isSearch)) {
            return new Info(false, max, min);
        }
        // 左边的值大于等于当前值 或者 右边的值小于当前值
        if((l != null && l.max >= node.value) || (r != null && r.min <= node.value)) {
            return new Info(false, max, min);
        }
        return new Info(true, max, min);
    }
    
    public static class Info{
        public boolean isSearch;
        public int max;
        public int min;

        public Info(boolean isSearch, int max, int min) {
            this.isSearch = isSearch;
            this.max = max;
            this.min = min;
        }
    }

十二、返回整颗二叉树节点与节点间的最大距离

所有会出现的情况

1、节点可能不经过头节点

二叉树左树和右树的最大的距离

2、会经过头节点的最大距离

左树最远（左高）+右树最远（右高）+1

代码实现

    public static int getMaxDistance(Node node) {
        if(node == null) {
            return 0;
        }
        return process(node).maxDistance;
    }

    private static Info process(Node node) {
        if(node == null) {
            return new Info(0, 0);
        }

        Info l = process(node.left);
        Info r = process(node.right);
        // 获取最孩子和右孩子的最大高度
        int height = Math.max(l.height, r.height) + 1;
        // 最孩子的高度+右孩子的高度就是头节点最大距离
        int headDistance = l.height + r.height + 1;
        // 头节点、左孩子最大距离、右孩子最大距离的最大距离
        int maxDistance = Math.max(l.maxDistance, Math.max(r.maxDistance, headDistance));
        return new Info(maxDistance, height);
    }

十三、满二叉树

数的高度是h，那2^h -1 = 节点数

    public static boolean isFull(Node node) {
        if(node == null) {
            return true;
        }
        Info info = process(node);
        return (1 << info.height) - 1 == info.nodeSize;
    }


    private static Info process(Node node) {
        if(node == null) {
            return new Info(0, 0);
        }
        Info l = process(node.left);
        Info r = process(node.right);
        int height = Math.max(l.height, r.height) + 1;
        int nodes = l.nodeSize + r.nodeSize + 1;
        return new Info(height, nodes);
    }


    private static class Info{

        public int height;

        public int nodeSize;

        public Info(int h, int n) {
            this.height = h;
            this.nodeSize = n;
        }
    }
 
    // 第二种方法
    // 收集子树是否是满二叉树
    // 收集子树的高度
    // 左树满 && 右树满 && 左右树高度一样 -> 整棵树是满的
    public static class Info2 {
        public boolean isFull;
        public int height;

        public Info2(boolean f, int h) {
            isFull = f;
            height = h;
        }
    }

十四、找到二叉树中最大的搜索二叉树

给定二叉树的子树是搜索二叉树的节点数最大值是多少，子二叉树必须是整棵树。

所有会出现的情况

1、头节点不是搜索二叉树

左树上的搜索二叉树的最多节点数
右树上的搜索二叉树的最多节点数

2、头节点是搜索二叉树

整个树的节点数

代码实现

    public static int getLargestBSTSubtree(TreeNode node) {
        if(node == null) {
            return 0;
        }
        return process(node).maxSubtreeSize;
    }

    public static Info process(TreeNode node) {
        if(node == null) {
            return null;
        }
        Info l = process(node.left);
        Info r = process(node.right);
        int allSize = 1;
        int max = node.val;
        int min = node.val;

        // 左节点不为空，则获取所有节点数量、最大值、最小值
        if(l != null){
            allSize += l.allSize;
            max = Math.max(max, l.max);
            min = Math.min(min, l.min);
        }

        // 右节点不为空，则获取所有节点数量、最大值、最小值
        if(r != null) {
            allSize += r.allSize;
            max = Math.max(max, r.max);
            min = Math.min(min, r.min);
        }

        // 获取左节点是否为搜索树、左节点最大搜索树节点数
        int p1 = -1;
        boolean leftBST = true;
        if(l != null){
            p1 = l.maxSubtreeSize;
            leftBST = l.maxSubtreeSize == l.allSize;
        }

        // 获取右节点是否为搜索树、右节点最大搜索树节点数
        int p2 = -1;
        boolean rightBST = true;
        if(r != null) {
            p2 = r.maxSubtreeSize;
            rightBST = r.maxSubtreeSize == r.allSize;
        }

        // 如果左右两边都是搜索树
        int p3 = -1;
        if(leftBST && rightBST) {
            int leftMax = l == null ? 0 : l.max;
            int rightMin = r == null ? 0 : r.min;
            // 如果整颗树都是搜索二叉树，则最大搜索树的节点树=左树节点树+右树节点树+1
            if(leftMax < node.val && rightMin > node.val) {
                p3 =(r== null ? 0 : r.maxSubtreeSize) + (l == null ? 0 : l.maxSubtreeSize) + 1;
            }
        }
        return new Info(Math.max(p1, Math.max(p2, p3)), allSize, max, min);
    }


    public static class Info{

        public int maxSubtreeSize;
        public int allSize;
        public int max;
        public int min;

        public Info(int maxSubtreeSize, int allSize, int max, int min) {
            this.maxSubtreeSize = maxSubtreeSize;
            this.allSize = allSize;
            this.max = max;
            this.min = min;
        }
    }

    // 提交时不要提交这个类
    public static class TreeNode {
        public int val;
        public TreeNode left;
        public TreeNode right;

        public TreeNode(int value) {
            val = value;
        }
    }

另外一题是返回头节点，其他条件一样

十五、给定头节点和AB两个节点求AB两个最初公共祖先

a节点和b接口往上找汇聚的第一个节点

所有会出现的情况

1、汇聚的节点不是头节点

已经在左树上汇聚了
已经在右树上汇聚了
a和b都没有找全

2、汇聚的节点是头节点

左树发现一个、右树发现另一个
头节点本身就是a节点，左树右树发现了节点b
头节点本省就是b节点，左树右树发现了节点a

3、上面的情况都没有匹配上则没有公共祖先

每个数需要的信息
1、树上有没有发现a
2、树上有没有发现b
3、树上发现的最低公共祖先（答案）

代码实现

    private static Info process(Node head, Node a, Node b) {
        if(head == null) {
            return new Info(false, false, null);
        }
        Info l = process(head.left, a, b);
        Info r = process(head.right, a, b);
        // 头节点是a 或者 左右节点找到a
        boolean findA = (head == a) || l.findA || r.findA;
        // 头节点是b 或者 左右节点找到b
        boolean findB = (head == b) || l.findB || r.findB;
        Node ans = null;
        if(l.ans != null) {
            ans = l.ans;
        } else if(r.ans != null) {
            ans = r.ans;
        } else {
            // 左右都没有找到汇聚节点，但是左边和右边都找到了值，则头节点就是汇聚节点
            if(findA && findB) {
                ans = head;
            }
        }
        return new Info(findA, findB, ans);
    }

    private static class Info{

        private boolean findA;
        private boolean findB;
        private Node ans;

        public Info(boolean findA, boolean findB, Node ans) {
            this.findA = findA;
            this.findB = findB;
            this.ans = ans;
        }
    }

十六、派对的最大快乐值

公司现在要办party，你可以决定哪些员工来，哪些员工不来，规则：

如果某个员工来了，那么这个员工的所有直接下级都不能来
派对的整体快乐值是所有到场员工快乐值的累加
你的目标是让派对的整体快乐值尽量大给定一棵多叉树的头节点boss，请返回派对的最大快乐值。

所有会出现的情况

1、当前节点参加派对

当前节点的快乐值+sum（子节点不参加派对的快乐值）

2、当前节点不参加派对

sum（max（子节点参加派对的快乐值，子节点不参加派对的快乐值））

需要的参数：参加派对的快乐值、不参加派对的快乐值

代码实现

    private static Info process(Employee e) {
        if(e == null) {
            return new Info(0, 0);
        }

        int yes = e.happy;
        int no = 0;
        for (Employee next : e.nexts) {
            Info process = process(next);
            // 当前节点不参加 = sum（max（yes，no））
            no += Math.max(process.yes, process.no);
            // 当前节点参加=sum（子节点不参加的快乐值）
            yes += process.no;
        }
        return new Info(yes, no);
    }

    private static class Info{

        public int yes;
        public int no;

        public Info(int yes, int no) {
            this.yes = yes;
            this.no = no;
        }
    }

04_二叉树学习

# 一、链表递归实现先序、中序、后序

# 二、链表非递归实现先序、中序、后序

# 先序

# 中序

# 后序

# 三、二叉树按层遍历

# 四、二叉树的序列化和反序列化

# 先序序列

# 后序序列

# 按层序列

# 五、多叉树和二叉树互转

# 六、设计一个打印整棵树的函数

# 七、求二叉树最宽的层有多少个节点

# 使用Map

# 不使用Map

# 八、找到节点的后继节点

# 九、二叉树折纸问题

# 九、判断是否为完全二叉树

# 十、判断是否为平衡树

# 所有会出现的情况

# 代码实现

# 十一、判断是否为搜索二叉树

# 所有会出现的情况

# 代码实现

# 十二、返回整颗二叉树节点与节点间的最大距离

# 所有会出现的情况

# 代码实现

# 十三、满二叉树

# 十四、找到二叉树中最大的搜索二叉树

# 所有会出现的情况

# 代码实现

# 十五、给定头节点和AB两个节点求AB两个最初公共祖先

# 所有会出现的情况

# 代码实现

# 十六、派对的最大快乐值

# 所有会出现的情况

# 代码实现

一、链表递归实现先序、中序、后序

二、链表非递归实现先序、中序、后序

先序

中序

后序

三、二叉树按层遍历

四、二叉树的序列化和反序列化

先序序列

后序序列

按层序列

五、多叉树和二叉树互转

六、设计一个打印整棵树的函数

七、求二叉树最宽的层有多少个节点

使用Map

不使用Map

八、找到节点的后继节点

九、二叉树折纸问题

九、判断是否为完全二叉树

十、判断是否为平衡树

所有会出现的情况

代码实现

十一、判断是否为搜索二叉树

所有会出现的情况

代码实现

十二、返回整颗二叉树节点与节点间的最大距离

所有会出现的情况

代码实现

十三、满二叉树

十四、找到二叉树中最大的搜索二叉树

所有会出现的情况

代码实现

十五、给定头节点和AB两个节点求AB两个最初公共祖先

所有会出现的情况

代码实现

十六、派对的最大快乐值

所有会出现的情况

代码实现