18_segmentAndIndexTree
一、segmentTree
1、介绍
线段树是一种解决在区间内批量增加、更新、查询数组或列表里面的一种算法,主要方式是将数组转换成二叉树的结构后用懒更新的方式实现快速的更新和查询。如下是GPT的介绍
线段树(Segment Tree)是一种用于解决区间查询问题的数据结构。它主要被用于处理数组或者列表等数据结构的区间查询操作,例如求区间和、最大值、最小值等。
线段树的基本思想是将一个区间划分成若干个子区间,并为每个子区间维护一些预先计算好的信息。通过不断地二分递归地创建子节点,将整个区间划分成左右两部分,直到达到单个元素区间或者无法再进一步划分。
在线段树中,每个节点代表一个区间,根节点表示整个待查询的区间。每个节点保存着对应区间的相关信息,比如区间内元素之和、最大值、最小值等。通过对子区间合并(merge)这些信息,可以得到父节点的相关信息,最终得到根节点的信息,即整个区间的查询结果。
线段树的构建过程需要 O(n) 的时间复杂度,其中 n 是待查询区间的长度。一旦线段树构建完成,单次区间查询的时间复杂度为 O(logn),非常高效。线段树还支持更新操作,即在某个位置上修改原始数据后,只需要更新对应节点及其祖先节点的信息即可,时间复杂度同样为 O(logn)。
线段树广泛应用于各种需要高效处理区间查询的算法和问题,例如计算机图形学中的区域填充、区间覆盖等。它提供了一种有效的数据结构来解决这类问题,大大降低了时间复杂度并提高了算法的效率。
2、增加、更新、查询的线段树思路
1、初始化懒更新的数组,大小为原始数组的4倍,用于记录整棵树
2、递归将累加和构建成一棵树sum,参数为左下标l、右下标r、树的开始节点下标root
- 如果左小标等于右下标则说明是叶子节点,累加和直接返回当前左下标的值
- 获取l~r的中间数后,递归处理每个节点的累加和。 左节点=root*2,右节点=root*2+1
- 汇总当前root的累加和
3、在给定l~r范围内所有的值都增加c
- 判断当前范围是否在目标范围内,在范围内则直接进行懒更新。将值存放到lazy里面,并计算新的累加和后更新。不更新范围里面的其他值
- 如果不在范围内则判断当前root是否存在懒更新数据,存在则将懒更新数据更新到左右节点上面
- 判断左右两边如果需要处理则递归处理范围数据(获取中间值后左右两边进行判断)
- 汇总累加和即可
3、代码
给定一个数组arr,用户希望你实现如下三个方法
1)void add(int L, int R, int V) : 让数组arr[L…R]上每个数都加上V
2)void update(int L, int R, int V) : 让数组arr[L…R]上每个数都变成V
3)int sum(int L, int R) :让返回arr[L…R]这个范围整体的累加和怎么让这三个方法,时间复杂度都是O(logN)
public static class SegmentTree{
private int maxn;
// 从1开始的数组
private int[] arr;
// 线段树区间和,范围累加和信息
private int[] sum;
// 线段树懒加载标记, 懒更新数据
private int[] lazy;
// 记录范围内有所有值都更新为一个值update
private int[] change;
// 更新的懒加载标记,记录更新的操作方式,解决相同值歧义问题
// false表示值无效0则表示没有update信息,true表示有效0则表示将所有值更新为0
private boolean[] updateLazy;
// 初始化线段树
public SegmentTree(int[] origin) {
maxn = origin.length + 1;
// 将原始数据放到arr里面
arr = new int[maxn];
for (int i = 1; i < maxn; i++) {
arr[i] = origin[i - 1];
}
sum = new int[maxn * 4];
lazy = new int[maxn * 4];
change = new int[maxn * 4];
updateLazy = new boolean[maxn * 4];
}
// 累加和build: 原始数据arr的下标l~r范围的数据,build到sum数组从rt位置开始
public void build(int l, int r, int root) {
// 叶子节点
if(l == r) {
sum[root] = arr[l];
return;
}
int mid = (l + r) / 2;
// 左边的值build
build(l, mid, root * 2);
// 右边的值build
build(mid + 1, r, root * 2 + 1);
// 计算当前值的累加和
pushUp(root);
}
// 获取当前节点的累加和(左孩子+右孩子)
private void pushUp(int rt) {
// 左孩子下标=i*2, 右孩子下标i*2+1
sum[rt] = sum[rt * 2] + sum[rt * 2 + 1];
}
/**
* 线段内的值都增加c,例子:
* 在1~1000的元素数组里面,3(l)~385(r)范围的值都增加c。树拆分的时候
* 1(left)~500(right)构建到sum的1(rt)下标里
* 501(left)~1000(right)构建到sum的2(rt)下标里
* @param l 当前线段的左边 (任务)
* @param r 当前线段的右边 (任务)
* @param C 线段里面的数需要累加的值 (任务)
* @param left 当前处理的左下标 (范围)
* @param right 当前处理的右下标 (范围)
* @param rt sum的根下标 (范围)
*/
public void add(int l, int r, int C, int left, int right, int rt) {
// 可以懒更新时, 如当前处理范围是3~385, 目标是1~500范围上都加上5。 范围的值全部在任务里面
if(l <= left && right <= r) {
// 所有值的累加和汇总赋值
sum[rt] += C * (right - left + 1);
// 进行懒更新
lazy[rt] += C;
return;
}
// 如果不能懒更新时,则获取当前值的中间值,并往下一层进行懒更新
int mid = (left + right) / 2;
// 结清之前的任务
pushDown(rt, mid - left + 1, (right - mid));
// 左边的新任务下发
if(l <= mid) {
add(l, r, C, left, mid, rt * 2);
}
// 右边的新任务下发
if(r > mid) {
add(l, r, C, mid + 1, right, rt * 2 + 1);
}
// 汇总当前值的累加和
pushUp(rt);
}
/**
* 往下面更新一层,当前层的懒更新放到左右两个子节点去进行懒更新
*
* @param root 当前处理的根节点
* @param ln 左边值的数量
* @param rn 右边值的数量
*/
private void pushDown(int root, int ln, int rn) {
int leftIndex = root * 2;
int rightIndex = root * 2 + 1;
// root节点存在更新信息。 更新节点必须在前
if(updateLazy[root]) {
// 先将左右节点的懒加载标记为ture
updateLazy[leftIndex] = true;
updateLazy[rightIndex]= true;
// 将左右节点的更新数据改为root的值
change[leftIndex] = change[root];
change[rightIndex] = change[root];
// 左右两个懒累加和的值清空
lazy[leftIndex] = 0;
lazy[rightIndex] = 0;
// 累加值的值重新赋值
sum[leftIndex] = change[root] * ln;
sum[rightIndex] = change[root] * rn;
// root节点的懒加载数据标记为false
updateLazy[root] = false;
}
// 当前节点存在懒数据时
if(lazy[root] != 0) {
// 左孩子更新
lazy[leftIndex] += lazy[root];
sum[leftIndex] += lazy[root] * ln;
// 右孩子更新
lazy[rightIndex] += lazy[root];
sum[rightIndex] += lazy[root] * rn;
// 当前位置清空
lazy[root] = 0;
}
}
/**
* 线段内的所有值都更新为c,例子:
* 在1~1000的元素数组里面,3(l)~385(r)范围的值都更新为c。
* @param l 当前线段的左边 (任务)
* @param r 当前线段的右边 (任务)
* @param c 线段里面的数需要累加的值 (任务)
* @param left 当前处理的左下标 (范围)
* @param right 当前处理的右下标 (范围)
* @param root sum的根下标 (范围)
*/
public void update(int l, int r, int c, int left, int right, int root) {
// 范围都包含,懒更新
if(l <= left && right <= r){
updateLazy[root] = true;
change[root] = c;
sum[root] = c * (right - left + 1);
lazy[root] = 0;
return;
}
int mid = (right + left) / 2;
pushDown(root, mid - left + 1, right - mid);
if(l <= mid) {
update(l, r, c, left, mid, root * 2);
}
if(r > mid) {
update(l, r, c, mid + 1, right, root * 2 + 1);
}
pushUp(root);
}
// 获取线段之内的累加和
public long query(int l, int r, int left, int right, int root) {
if(l <= left && right <= r) {
return sum[root];
}
int mid = (left + right) / 2;
pushDown(root, mid - left + 1, right - mid);
long ans = 0;
if(l <= mid) {
ans += query(l, r, left, mid, root * 2);
}
if(r > mid) {
ans += query(l, r, mid + 1, right, root * 2 + 1);
}
return ans;
}
}
4、俄罗斯方块游戏
1、题目
想象一下标准的俄罗斯方块游戏,X轴是积木最终下落到底的轴线。下面是这个游戏的简化版:
1)只会下落正方形积木
2)[a,b] -> 代表一个边长为b的正方形积木,积木左边缘沿着X = a这条线从上方掉落
3)认为整个X轴都可能接住积木,也就是说简化版游戏是没有整体的左右边界的
4)没有整体的左右边界,所以简化版游戏不会消除积木,因为不会有哪一层被填满。
给定一个N*2的二维数组matrix,可以代表N个积木依次掉落,返回每一次掉落之后的最大高度
https://leetcode.com/problems/falling-squares/
2、思路
1、利用线段树的更新机制每次落下一个方块都更新最大值(修改线段树的机制为最大值)
2、每次查询当前落下方块区域的最大值后加上当前方块的值更新线段树
3、落下方块时为了保证不会出现相邻两个方块重叠,则右边界-1
3、代码
public static class SegmentTree{
private int[] max;
private int[] change;
public boolean[] update;
// 初始化数据,没有原始数据,直接初始化大小
public SegmentTree(int size) {
int n = size + 1;
max = new int[n * 4];
change = new int[n * 4];
update = new boolean[n * 4];
}
// 更新操作
public void update(int l, int r, int c, int left, int right, int root) {
// 进行懒更新
if(l <= left && right <= r) {
update[root] = true;
change[root] = c;
max[root] = c;
return;
}
// 获取中点下标
int mid = (left + right) / 2;
// 将懒更新往下移
pushDown(root);
// 左边往下递归更新
if(l <= mid) {
update(l, r, c, left, mid, root * 2);
}
// 右边往下递归更新
if(r > mid) {
update(l, r, c, mid + 1, right, root * 2 + 1);
}
// 计算当前值最大值
pushUp(root);
}
// 获取当前值最大值,通过左右子节点
private void pushUp(int root) {
max[root] = Math.max(max[root * 2], max[root * 2 + 1]);
}
// 将懒更新数据下移到左右节点
private void pushDown(int root) {
if(!update[root]) {
return;
}
int leftIndex = root * 2;
int rightIndex = leftIndex + 1;
// 左右节点更新标记为true
update[leftIndex] = true;
update[rightIndex] = true;
// 左右更新为父节点的值
change[leftIndex] = change[root];
change[rightIndex] = change[root];
max[leftIndex] = change[root];
max[rightIndex] = change[root];
update[root] = false;
}
// 查询最大值
public int query(int l, int r, int left, int right, int root) {
if(l <= left && right <= r) {
return max[root];
}
int mid = (left + right) / 2;
pushDown(root);
int result = -1;
if(l <= mid) {
result = Math.max(result, query(l, r, left, mid, root * 2));
}
if(r > mid) {
result = Math.max(result, query(l, r, mid + 1, right, root * 2 + 1));
}
return result;
}
}
// 获取每一步下降的正方形的最高点
public List<Integer> fallingSquares(int[][] positions) {
List<Integer> result = new ArrayList<>();
// 将边界方块值压缩,减少线段树长度
HashMap<Integer, Integer> map = index(positions);
// 初始化线段树
int n = map.size();
SegmentTree segmentTree = new SegmentTree(n);
int max = 0;
for (int[] position : positions) {
// 获取左边界
int l = map.get(position[0]);
// 获取右边界
int r = map.get(position[0] + position[1] - 1);
// 获取l~r范围上面的最大值高度: 查询当前方块位置的高度并加上当前方块的高度
int height = segmentTree.query(l, r, 1, n, 1) + position[1];
// 获取最大的方块高度
max = Math.max(max, height);
result.add(max);
// 将l~r范围的高度全部都更新为height
segmentTree.update(l, r, height, 1, n, 1);
}
return result;
}
public HashMap<Integer, Integer> index(int[][] positions) {
// 有序存入方块的左边边界和右边界的值
TreeSet<Integer> pos = new TreeSet<>();
for (int[] arr : positions) {
pos.add(arr[0]);
pos.add(arr[0] + arr[1] - 1);
}
HashMap<Integer, Integer> map = new HashMap<>();
int count = 0;
for (Integer index : pos) {
map.put(index, ++count);
}
return map;
}
总结:线段树主要是解决数组区域字段批量更新的场景,遇到这种场景就可以考虑使用线段树。先忙的indexTree也是批量更新区间值和查询的方式,区别点在于indexTree在解决二维或三维数组的区间更新和查询的效率要好很多。
二、indexTree
1、介绍
indexTree是一种利用二进制位数的计算从而找到一种能快速支持数组区间更新和查询数组一种方式,GPT介绍如下:
"indexTree" 是指索引树(Index Tree)的一种数据结构,也称为树状数组(Binary Indexed Tree)。
索引树是一种可以高效支持区间修改和区间查询操作的数据结构。它主要用于解决频繁更新某个序列中元素值,并需要快速计算区间和的问题。
索引树的基本思想是利用二进制的特性来维护区间和。对于一个长度为 n 的序列,索引树使用一个长度为 n+1 的数组来存储元素,并利用数组下标与二进制表示进行映射关系。
索引树的每个节点代表一段连续的元素区间,如节点 i 表示区间 [i-k+1, i],其中 k 是 i 的最低有效位所包含的连续 0 的个数。每个节点上存储了区间内元素的累加和,即从下标 i-k+1 到 i 的所有元素之和。
索引树的构建过程需要 O(nlogn) 的时间复杂度,其中 n 是序列的长度。但一旦构建完成后,单次区间查询的时间复杂度为 O(logn),单次区间修改的时间复杂度同样为 O(logn)。
索引树广泛应用于各种需要高效计算区间和的场景,例如范围求和查询、逆序对计数等。由于其较低的时间复杂度以及相对简单的实现,索引树成为了一种非常有用的数据结构。
2、代码
public static class IndexTree{
private int[] tree;
private int n;
// 0位置不使用
public IndexTree(int size) {
n = size;
tree = new int[n + 1];
}
/**
* 计算当前位置的累加和
*
* @param index 需要累加的位置
* @return 累加值
*/
public int sum(int index) {
int result = 0;
while (index > 0) {
result += tree[index];
// 将二进制的1去掉
index -= index & -index;
}
return result;
}
/**
* 在index位置上加上指定值
*
* @param index 指定下标位置上
* @param d 需要增加的值
*/
public void add(int index, int d) {
while (index <= n) {
// 依次更新受影响的数据
tree[index] += d;
// 计算出需要同步更新数据的位置,将index位置二进制的1依次加进去
index += index & -index;
}
}
3、二维数组的累加和计算
https://leetcode.com/problems/range-sum-query-2d-mutable
只是把代码copy过来,没有仔细理解。二进制替换找位置的方式只是记忆,没有搞清楚前因后果
public static class NumMatrix{
private int[][] tree;
private int[][] nums;
private int N;
private int M;
// 初始化二维数组
public NumMatrix(int[][] matrix) {
if (matrix.length == 0 || matrix[0].length == 0) {
return;
}
N = matrix.length;
M = matrix[0].length;
tree = new int[N + 1][M + 1];
nums = new int[N][M];
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
update(i, j, matrix[i][j]);
}
}
}
// 计算累加和
private int sum(int row, int col) {
int sum = 0;
for (int i = row + 1; i > 0; i -= i & (-i)) {
for (int j = col + 1; j > 0; j -= j & (-j)) {
sum += tree[i][j];
}
}
return sum;
}
// 更新二维数组里面的值
public void update(int row, int col, int val) {
if (N == 0 || M == 0) {
return;
}
int add = val - nums[row][col];
nums[row][col] = val;
for (int i = row + 1; i <= N; i += i & (-i)) {
for (int j = col + 1; j <= M; j += j & (-j)) {
tree[i][j] += add;
}
}
}
// 计算两个坐标之间的累加和
public int sumRegion(int row1, int col1, int row2, int col2) {
if (N == 0 || M == 0) {
return 0;
}
return sum(row2, col2) + sum(row1 - 1, col1 - 1) - sum(row1 - 1, col2) - sum(row2, col1 - 1);
}
}
三、AC自动机
1、介绍
AC自动机是一种高效寻找关键字的一种算法,主要逻辑是将关键组组装成前缀树,之后通过自动跳转到下一个可能出现的关键字节点从而实现快速匹配的效果.
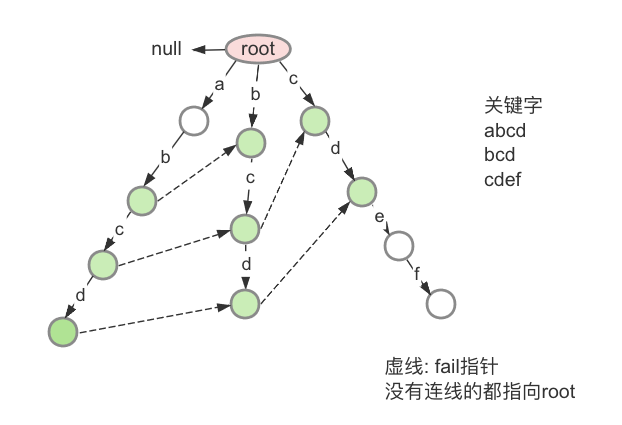
GPT介绍:
AC自动机(Aho-Corasick Automaton)是一种用于多模式匹配的字符串匹配算法。它可以高效地在一个文本中同时匹配多个模式串,并找到所有的匹配结果。
AC自动机的基本思想是构建一个有限状态自动机,在该自动机中每个节点表示已经匹配的模式串前缀,边表示字符转移。通过使用一些特定的数据结构和算法,AC自动机可以在匹配过程中自动跳转到下一个可能的状态,从而实现高效的多模式匹配。
AC自动机的构建过程大致可以分为以下几个步骤:
构建Trie树:将所有模式串构建成一棵Trie树,使得每个节点表示一个模式串的前缀,从根节点开始的路径表示模式串的匹配过程。
添加失败指针(Failure Pointer):对每个节点设置一个失败指针,指向在Trie树中与当前节点相匹配且长度更短的字符串的最长后缀节点。
添加输出指针(Output Pointer):对每个节点设置一个输出指针,指向与当前节点匹配的模式串列表。当匹配到某个节点时,依次沿着输出指针找到所有匹配的模式串。
进行状态转移:遍历文本字符序列,根据当前字符以及自动机的状态转移规则进行状态转移,并输出匹配的结果。
AC自动机可以应用于许多字符串处理问题,如关键词过滤、字典匹配、DNA序列分析等。它具有快速匹配、高效利用内存和线性时间复杂度的特点。
2、思路
1、将每个关键字单独组装成前缀树
2、利用endUse字段标记字段是否使用过,end字段便于收集关键字返回
3、最主要的逻辑是fail指针
3、代码
public static class ACAutomation{
private Node root;
public ACAutomation() {
root = new Node();
}
/**
* 插入关键字,建立前缀树
*
* @param s 关键字字符串
*/
public void insert(String s) {
char[] chars = s.toCharArray();
Node cur = root;
int index = 0;
// 遍历字符
for (int i = 0; i < chars.length; i++) {
// 计算出当前字符的位置
index = chars[i] - 'a';
// 如果位置上面的值为空则创建节点
if(cur.nexts[index] == null) {
cur.nexts[index] = new Node();
}
// 当前节点赋值为index位置
cur = cur.nexts[index];
}
cur.end = s;
}
/**
* 构建fail指向
*/
public void build() {
// 宽度优先遍历
Queue<Node> queue = new LinkedList<>();
queue.add(root);
Node cur = null;
Node currentFail = null;
while (!queue.isEmpty()) {
// 弹出父节点并获取它的子指针并指向cur(父找子)
cur = queue.poll();
// 遍历26个字母
for (int i = 0; i < 26; i++) {
// i不存在则往后寻找
if(cur.nexts[i] == null){
continue;
}
// 将fail先指向root,找到fail则指向
cur.nexts[i].fail = root;
// 当前父节点的fail指针赋值给currentFail
currentFail = cur.fail;
// 当前父指针不为空
while (currentFail != null) {
// 当前父指针的子节点存在i字符
if(currentFail.nexts[i] != null) {
// 将当前子节点的i位置的fail指针指向 当前父指针子节点的i字符
cur.nexts[i].fail = currentFail.nexts[i];
break;
}
// 一直往fail指针循环找
currentFail = currentFail.fail;
}
queue.add(cur.nexts[i]);
}
}
}
// 查找字符串context的关键字
public List<String> containWords(String content) {
char[] chars = content.toCharArray();
Node cur = root, follow = null;
int index = 0;
List<String> result = new ArrayList<>();
// 遍历content字符
for (int i = 0; i < chars.length; i++) {
// 获取字符的路
index = chars[i] - 'a';
// 通过tail指针往后寻找如果一直没有找到关键字则cur指向fail
while (cur.nexts[index] == null && cur != root) {
// 赋值为fail指针
cur = cur.fail;
}
// 当前节点没有找到路则指向root
cur = cur.nexts[index] != null ? cur.nexts[index] : root;
// 通过fail指针往后遍历查找关键字
follow = cur;
while (follow != root) {
// 使用过则往后执行
if(follow.endUse) {
break;
}
// 如果当前节点的end值不为空则命中关键字
if(follow.end != null) {
result.add(follow.end);
// 标记以获取
follow.endUse = true;
}
// 往后寻找其他关键字
follow = follow.fail;
}
}
return result;
}
}
public static class Node{
// 某个字符串的结尾,值就是字符串
private String end;
// 记录这个节点之前有没有使用过
private Boolean endUse;
// 指向相同节点的指针,没有则指向头节点
private Node fail;
// 下一个节点列表
private Node[] nexts;
public Node() {
endUse = false;
end = null;
fail = null;
nexts = new Node[26];
}
}