09_动态规划
遇到重复调用的过程,将过程的结果记录下来,下次遇到直接获取结果的操作就是动态规划(空间换时间)。
先从尝式(暴力)开始,之后优化为动态规划
一、斐波那契数列
1 题目
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”。 斐波那契数列指的是这样一个数列:1,1,2,3,5,8,13,21,34,55,89... 这个数列从第3项开始,每一项都等于前两项之和。
2 递归实现
public static int fibonacci(int n) {
if(n == 1 || n == 2) {
return 1;
}
//当n >=3时有, Fn = (Fn-1) + (Fn-2)
return fibonacci(n -1 ) + fibonacci((n -2));
}
每次计算的时候都会有重复值的计算,将重复计算的结果放入缓存中用于减少每次的计算就是DP动态规划。斐波那契数列由于计算简单所以加上缓存也没有减少多少计算量。
二、机器人到达目标位置步数
1 题目
假设有排成一行的N个位置,记为1~N,N 一定大于或等于 2。 开始时机器人在其中的M位置上(M 一定是 1~N 中的一个)。如果机器人来到1位置,那么下一步只能往右来到2位置;如果机器人来到N位置,那么下一步只能往左来到 N-1 位置;如果机器人来到中间位置,那么下一步可以往左走或者往右走;规定机器人必须走 K 步,最终能来到P位置(P也是1~N中的一个)的方法有多少种给定四个参数 N、M、K、P,返回方法数。
2 思路
1、步数走完:当前位置就是目标位置则有一种方式,否则当前方式不行
2、当前位置是1:没办法往左走就等于从2开始往右(步数减1)的所有情况
3、当前位置是n:没办法往右走就等于从n-1往左(步数减-)的所有情况
4、中间位置:往左走和往后走的和就是所有的情况
演变方式从暴力递归 > 缓存dp表 > 二维动态规划表(状态转移),的方式完成该算法。
3 递归方式
/**
* 机器人递归计算方式
*
* 1、机器人只能一步一步走
* 2、如果机器人在位置1,那么下一步只能到位置2
* 3、如果机器人在位置n,那么下一步只能到位置n-1
* 4、如果机器人位置在中间,那么下一步能到n+1和n-1的位置
*
* @param n 排成一行的n个位置
* @param m 机器人的当前位置
* @param k 机器人能走的步数
* @param p 需要到达的目标位置
* @return 有多少种方法能达到目标位置
*/
public static int process(int n, int m, int k, int p) {
// 步数走完,如果到达目标位置则当前方法有效
if(k == 0) {
return m == p ? 1 : 0;
}
// 机器人在位置1只能到m+1位置
if(m == 1) {
return process(n, 2, k - 1, p);
}
// 机器人在位置n只能到m-1位置
if(m == n) {
return process(n, m - 1, k - 1, p);
}
// 机器人在中间位置则步数 =(m+1位置的数量) + (m-1位置的数量)
return process(n, m + 1, k - 1, p) + process(n, m - 1, k - 1, p);
}
4 缓存DP
/**
* 机器人缓存计算方式
*
* 1、机器人只能一步一步走
* 2、如果机器人在位置1,那么下一步只能到位置2
* 3、如果机器人在位置n,那么下一步只能到位置n-1
* 4、如果机器人位置在中间,那么下一步能到n+1和n-1的位置
*
* @param n 排成一行的n个位置
* @param m 机器人的当前位置
* @param k 机器人能走的步数
* @param p 需要到达的目标位置
* @return 有多少种方法能达到目标位置
*/
public static int process1(int n, int m, int k, int p) {
// 初始化数据,-1的表示没有缓存
int[][] dp = new int[n + 1][k + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= k; j++) {
dp[i][j] = -1;
}
}
return processCache(n, m, k, p, dp);
}
// 缓存DP
private static int processCache(int n, int m, int k, int p, int[][] dp) {
// 如果存在缓存则返回缓存数据
if(dp[n][k] != -1) {
return dp[n][k];
}
int walks = 0;
// 步数走完,如果到达目标位置则当前方法有效
if(k == 0) {
walks = m == p ? 1 : 0;
}
// 机器人在位置1只能到m+1位置
else if(m == 1) {
walks = process(n, 2, k - 1, p);
}
// 机器人在位置n只能到m-1位置
else if(m == n) {
walks = process(n, m - 1, k - 1, p);
}
// 机器人在中间位置则步数 =(m+1位置的数量) + (m-1位置的数量)
else {
walks = process(n, m + 1, k - 1, p) + process(n, m - 1, k - 1, p);
}
dp[n][k] = walks;
return walks;
}
5 动态规划状态转移
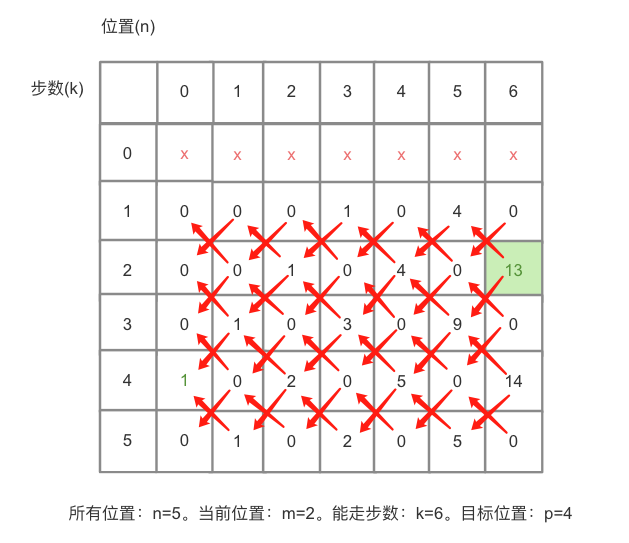
结合递归方式分析数据,例子:所有的位置n=5, 机器人当前位置m=2,机器人能走的步数k=6,目标位置p=4。
1、位置n等于0的一直不会有值
2、机器人当前位置是2,走6步到目标位置是4。
3、目标位置k=0时候,n=4的值为1,其余的n为0。
4、机器人当前位置是1时,需要走的总步数依赖n=2,k-1。
5、机器人当前位置是n时,需要走的总步数依赖n-1,k-1。
6、机器人当前位置是其他值时,需要走的总步数是【n=2,k-1】的步数加上【n-1,k-1】的步数。
/**
* 通过递归分析后可以直接生成DP表,生成之后直接获取值即可
*
* @param n 排成一行的n个位置
* @param m 机器人的当前位置
* @param k 机器人能走的步数
* @param p 需要到达的目标位置
* @return 有多少种方法能达到目标位置
*/
public static int process2(int n, int m, int k, int p) {
int[][] dp = new int[n + 1][k + 1];
// 目标位置k=0时候,n=4的值为1,其余的n为0
dp[p][0] = 1;
// 遍历步数,一列一列计算,第一列以及获取到值
for (int i = 1; i <= k; i++) {
// 机器人当前位置是1时,需要走的总步数依赖n=2,k-1。
dp[1][i] = dp[2][i -1];
// 机器人当前位置是n时,需要走的总步数依赖n-1,k-1。
dp[n][i] = dp[n-1][i-1];
// 位置n等于0的一直不会有值,n=1的也计算过,故从n=2开始
for (int j = 2; j < n; j++) {
// 机器人当前位置是其他值时,需要走的总步数是【n=2,k-1】的步数加上【n-1,k-1】的步数
dp[j][i] = dp[j-1][i-1] + dp[j+1][i-1];
}
}
// 直接返回位置上的数据即可
return dp[m][k];
}
三、给定整型数组arr纸牌方式获取最大分数
1 题目
给定一个整型数组arr,代表数值不同的纸牌排成一条线。玩家A和玩家B依次拿走每张纸牌。规定玩家A先拿,玩家B后拿,但是每个玩家每次只能拿走最左或最右的纸牌。玩家A和玩家B都绝顶聪明,请返回最后获胜者的分数。
2 思路
1、最后只剩余一张牌时,先手获取,后手获取0
2、先手有两种选择,一个是选左边的值加上站在后手的角度获取值(忍一手的情况)。另一个就是选右边的值加上站在后手的角度获取值(忍一手的情况)。获取最大的值就是先手值。
3、后手也有两种选择,一种是用先手的方式获取左,一种是用先手的方式获取右,之后取最小的(最大倍先手已经获取了)
3 递归方式
public static int win(int[] arr) {
int b = before(arr, 0, arr.length -1);
int a = after(arr, 0, arr.length-1);
return Math.max(a, b);
}
// 先拿有两种情况,1、拿左边的值+ 后手获取的最大值。 2、拿右边的值 + 后手获取的最大值
public static int before(int[] arr, int left, int right) {
// 最后一张牌直接获取
if(left == right) {
return arr[left];
}
// 先拿左边的 + 对手拿了之后剩余的后手(left+1)
int l = arr[left] + after(arr, left + 1, right);
// 先拿右边的 + 对手拿了之后剩余的后手(right-1)
int r = arr[right] + after(arr, left, right -1);
return Math.max(l, r);
}
// 后拿
public static int after(int[] arr, int left, int right) {
// 只有一张牌,无法获取
if(left == right) {
return 0;
}
// 拿左边的先手值(对手拿了右边的值)
int l = before(arr, left, right - 1);
// 拿右边的先手值(对手拿走了左边的值)
int r = before(arr,left + 1, right);
// 获取最小的值
return Math.min(l, r);
}
4 缓存DP
观察主函数,递归处理时候是一直在分解数组,两边都有相同的值则可以用缓存表提升效率。互相依赖的两个函数可以直接用两个表缓存,则利用两张二维数组创建dp缓存表,长宽都是数组的长度
public static int win1(int[] arr) {
int n = arr.length;
int[][] beforeDp = new int[n][n];
int[][] afterDp = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
beforeDp[i][j] = -1;
afterDp[i][j] = -1;
}
}
int b = beforeCache(arr, 0, arr.length -1, beforeDp, afterDp);
int a = afterCache(arr, 0, arr.length-1, beforeDp, afterDp);
return Math.max(a, b);
}
// 先拿有两种情况,1、拿左边的值+ 后手获取的最大值。 2、拿右边的值 + 后手获取的最大值
public static int beforeCache(int[] arr, int left, int right, int[][] beforeDp, int[][] afterDp) {
if(beforeDp[left][right] != -1) {
return beforeDp[left][right];
}
// 最后一张牌直接获取
int result = 0;
if(left == right) {
result = arr[left];
} else {
// 先拿左边的 + 对手拿了之后剩余的后手(left+1)
int l = arr[left] + afterCache(arr, left + 1, right, beforeDp, afterDp);
// 先拿右边的 + 对手拿了之后剩余的后手(right-1)
int r = arr[right] + afterCache(arr, left, right -1, beforeDp, afterDp);
result = Math.max(l, r);
}
beforeDp[left][right] = result;
return result;
}
// 后拿
public static int afterCache(int[] arr, int left, int right, int[][] beforeDp, int[][] afterDp) {
if(afterDp[left][right] != -1) {
return afterDp[left][right];
}
// 只有一张牌,无法获取
int result = 0;
if(left != right) {
// 拿左边的先手值(对手拿了右边的值)
int l = beforeCache(arr, left, right - 1, beforeDp, afterDp);
// 拿右边的先手值(对手拿走了左边的值)
int r = beforeCache(arr,left + 1, right, beforeDp, afterDp);
// 获取最小的值
result = Math.min(l, r);
}
afterDp[left][right] = result;
return result;
}
5 动态规划状态转移
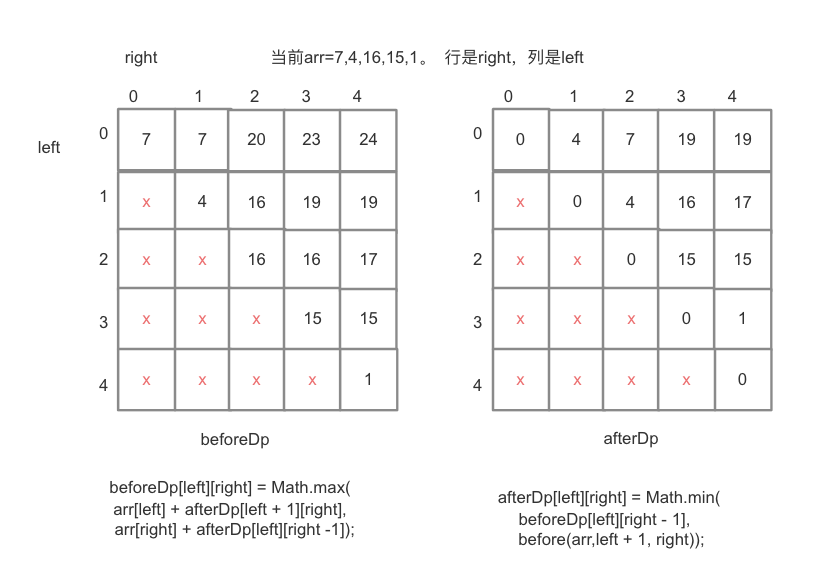
例:当前数组7,4,16,15,1
1、left=right时先手获取当前数组上的值,后手的值为0
2、left>right是不可能出现的,打叉
3、before表依赖当前值对称after表的left+1和right-1
4、after表依赖当前值对称的before表的left+1和right-1
5、before和after互相计算值
public static int win2(int[] arr) {
if(arr == null || arr.length < 1) {
return 0;
}
int n = arr.length;
// 初始化after的有效值
int[][] beforeDp = new int[n][n];
int[][] afterDp = new int[n][n];
for (int i = 0; i < n; i++) {
beforeDp[i][i] = arr[i];
}
for (int i = 1; i < n; i++) {
int left = 0;
int right = i;
// 行不会越界,只需要判断列即可
while (right < n) {
// 之前从递归中取,缓存从dp中取
System.out.println( arr[left]);
System.out.println(afterDp[left + 1][right]);
beforeDp[left][right] = Math.max(
// 先拿左边的 + 对手拿了之后剩余的后手(left+1)
arr[left] + afterDp[left + 1][right],
// 先拿右边的 + 对手拿了之后剩余的后手(right-1)
arr[right] + afterDp[left][right -1]);
// 获取最小的值
afterDp[left][right] = Math.min(
// 拿左边的先手值(对手拿了右边的值)
beforeDp[left][right - 1],
// 拿右边的先手值(对手拿走了左边的值)
before(arr,left + 1, right));
left++;
right++;
}
}
return Math.max(
// 先手获取的最大值
beforeDp[0][arr.length -1],
// 后手获取的最大值
afterDp[0][arr.length-1]);
}
四、背包问题
1 题目
给定两个长度都为N的数组weights和values,weights[i]和values[i]分别代表 i号物品的重量和价值。给定一个正数bag,表示一个载重bag的袋子,你装的物品不能超过这个重量。返回你能装下最多的价值是多少?
2 思路
1、只需要计算从第一个货物开始往后的每个货物的重量放入背包后的价值最大,后面的每个获取有如下两种情况
2、货物放入背包中,获取的最大价值
3、货物不放入背包中,获取的最大价值
4、之后就是计算两种情况的最大价值
3 递归
public static int maxValue(int[] w, int[] v, int bag) {
// 数据有效检查
if(w == null || v == null || w.length != v.length || w.length < 1) {
return 0;
}
// 下标从0开始计算货物最大价值
return process(w, v, 0, bag);
}
/**
* 递归处理背包问题
*
* @param w 重量数组
* @param v 价值数组
* @param index 当前处理货物的下标
* @param bag 当前背包数量
* @return 当前下标往后的最大价值, -1表示背包放不下了
*/
private static int process(int[] w, int[] v, int index, int bag) {
// 背包装完了
if(bag < 0) {
return -1;
}
// 货物装完了
if(index == w.length) {
return 0;
}
// 不要当前的货物
int p1 = process(w, v, index + 1, bag);
// 要当前的获取
int p2 = process(w, v, index + 1, bag - w[index]);
// 如果背包容量不够则价值为0,否则价值等于下一个最大价值加上当前下标价值
p2 = p2 == -1 ? 0 : p2 + v[index];
return Math.max(p1, p2);
}
4 动态规划
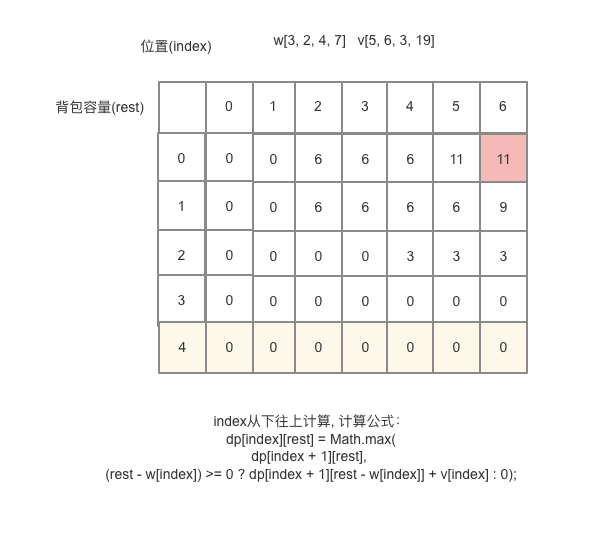
1、可变参数:观察到当前递归的可变参数是下标和背包容量
2、之后查看是否存在重复调用情况,每次往后在同一个下标上是可能出现相同重量的,例如:
w[3,2,5,.,.,.]
v[3,4,6,.,.,.]
当下标是2时,下面两种场景就是重复的参数process(w,v,2, 5)
获取的重量要下标0,1,不要2
获取的重量不要下标0,1,要3
3、当index=w.length时就是index的最后一行全部是0
4、当前index依赖下一个index的值,最后一行已经有了。只需要从后往前推就可以了
public static int dp(int[] w, int[] v, int bag) {
// 数据有效检查
if (w == null || v == null || w.length != v.length || w.length < 1) {
return 0;
}
int n = w.length;
int[][] dp = new int[n + 1][bag + 1];
for (int index = n - 1; index >= 0; index--) {
for (int rest = 0; rest <= bag; rest++) {
int p1 = dp[index + 1][rest];
// 如果背包容量不够则价值为0,否则价值等于下一个最大价值加上当前下标价值
int p2 = 0;
// 剩余背包重量
int re = rest - w[index];
if(re >= 0) {
// 当前货物价值加上index+1的价值
p2 = dp[index + 1][re] + v[index];
}
// 赋值
dp[index][rest] = Math.max(p1, p2);
}
}
return dp[0][bag];
}
五、字符转化
1 题目
规定1和A对应、2和B对应、3和C对应...26和Z对应。 那么一个数字字符串比如"111”就可以转化为:"AAA"、"KA"和"AK"。给定一个只有数字字符组成的字符串str,返回有多少种转化结果
2 思路
从左往右的尝试模型
1、能走到最后一个字符,则说明匹配上
2、当前字符是‘0’则未匹配上
3、获取匹配上下一个字符的数据
4、如果下下一个字符存在则也获取后累加
3 递归
/**
* 递归尝试(没给字符都和后面的所有字符匹配)
*
* @param chars 所有的字符
* @param index 当前是第几个字符
* @return 匹配到的字符数量
*/
private static int process(char[] chars, int index) {
// 走到最后一个字符了,说明前面一直有字符!='0',则当前字符匹配上
if(chars.length == index) {
return 1;
}
// 只有1~26个字符,如果存在0字符则当前分支未匹配上
if(chars[index] == '0') {
return 0;
}
// 递归获取下一个字符的所有匹配数
int val = process(chars, index +1);
// 没有越界
if(index + 1 < chars.length
// 当前未和下一位的的和小于27
&& (chars[index] - '0') * 10 + chars[index + 1] - '0' < 27) {
val += process(chars, index + 2);
}
return val;
}
4 动态规划
1、分析可变参数只有一个下标index,一个一维数组即可
2、index=chars.length时的值为1, 从右往左遍历
3、index的值等于‘0’时处理下一个下标
4、将递归的函数放到dp里面进行调整
/**
* 动态规划处理
*
* @param str 需要处理的字符串
* @return 匹配的数量
*/
public static int dp(String str) {
if(str == null || str.isEmpty()){
return 0;
}
// 创建一维dp数组表
char[] chars = str.toCharArray();
int n = chars.length;
int[] dp = new int[n + 1];
// 根据递归函数得知下标为n的值为1
dp[n] = 1;
// 从右往左遍历,从n-1开始
for (int index = n -1; index >= 0; index--) {
// 只有1~26个字符,如果存在0字符则当前分支未匹配上
if(chars[index] == '0') {
continue;
}
// 递归方式是进行递归,此处从dp表获取
int val = dp[index +1];
// 没有越界
if(index + 1 < chars.length
// 当前未和下一位的的和小于27
&& (chars[index] - '0') * 10 + chars[index + 1] - '0' < 27) {
// 递归方式是进行递归,此处从dp表获取
val += dp[index + 2];
}
dp[index] = val;
}
// 根据递归主函数得知获取下标0的值即可
return dp[0];
}
六、贴纸(无法严格位置依赖)
1 题目
给定一个字符串str,给定一个字符串类型的数组arr,出现的字符都是小写英文arr每一个字符串,代表一张贴纸,你可以把单个字符剪开使用,目的是拼出str来返回需要至少多少张贴纸可以完成这个任务。无效解返回-1
例子:str= "babac",arr = {"ba","c","abcd"}
答案:ba + ba + c 3 abcd + abcd 2 abcd+ba 2所以返回2
https://leetcode.com/problems/stickers-to-spell-word
2 思路
1、将给定字符排序后,将给的贴纸每一张都作为第一张全部尝试,获取最小的贴纸数量
2、排序后的命中率要高一些
3、目标为0时,结束递归
4、遍历所有贴纸,依次从给定str中减去存在的字符,存在匹配字符则递归处理后面的贴纸
5、获取最小贴纸数后返回
3 递归
/**
* 获取最小贴纸
*
* @param stickers 所有的贴纸
* @param target 最终需要剪的值
* @return 最小贴纸数量
*/
public static int minStickers(String[] stickers, String target) {
if(stickers == null || stickers.length < 1 || target == null || target.isEmpty()) {
return 0;
}
int ans = process(stickers, target);
return Integer.MAX_VALUE == ans ? -1 : ans;
}
/**
* 递归获取贴纸数量
*
* @param stickers 所有的贴纸
* @param target 最终需要剪的值
* @return 最小贴纸数量
*/
private static int process(String[] stickers, String target) {
// 没有需要拼接的贴纸,直接返回0
if(target.isEmpty()) {
return 0;
}
int min = Integer.MAX_VALUE;
for (String sticker : stickers) {
String rest = minus(target, sticker);
// 当前贴纸没有一个符合
if(rest.length() == target.length()) {
continue;
}
// 递归获取剩余字符的最小贴纸数量
min = Math.min(min, process(stickers, rest));
}
// 如果没有贴纸符合则返回最大integer, 否则最小贴纸数量加上当前字符数量
return min + (min == Integer.MAX_VALUE ? 0 : 1);
}
/**
* 减去贴纸后获取剩余的字符
*
* @param target 需要的字符
* @param sticker 贴纸上面的字符
* @return 减去后剩余的字符
*/
private static String minus(String target, String sticker) {
char[] targets = target.toCharArray();
char[] stickers = sticker.toCharArray();
int[] counts = new int[26];
// 将字符的数量放入数组中
for (char c : targets) {
counts[c-'a']++;
}
// 减去贴纸的字符数量
for (char c : stickers) {
counts[c-'a']--;
}
// 将剩余的字符组装为字符串
StringBuilder builder = new StringBuilder();
for (int i = 0; i < counts.length; i++) {
if(counts[i] > 0) {
for (int j = 0; j < counts[i]; j++) {
builder.append((char)(i + 'a'));
}
}
}
return builder.toString();
}
4 递归优化
1、用二维数组代替贴纸数组,减起来快
2、剪枝:每次跑的时候都必须包含第一个字符
/**
* 递归处理贴纸(用二维数组优化版-剪枝)
*
* @param stickers 所有的贴纸
* @param target 最终需要剪的值
* @return 最小贴纸数量
*/
public static int minStickers1(String[] stickers, String target) {
int n = stickers.length;
// 将贴纸转化为二维数组
int[][] counts = new int[n][26];
for (int i = 0; i < n; i++) {
char[] chars = stickers[i].toCharArray();
for (int i1 = 0; i1 < chars.length; i1++) {
counts[i][chars[i1] - 'a'] ++;
}
}
// 递归获取最小贴纸
int ans = process1(counts, target);
return ans == Integer.MAX_VALUE ? -1 : ans;
}
/**
* 贴纸优化版本
*
* @param stickers 二维数组处理贴纸
* @param target 剩余需要匹配的字符
* @return 最小贴纸数量
*/
private static int process1(int[][] stickers, String target) {
if(target.length() == 0) {
return 0;
}
// 用一维数组转化target
char[] chars = target.toCharArray();
int[] targetCounts = new int[26];
for (char aChar : chars) {
targetCounts[aChar - 'a']++;
}
int n = stickers.length;
int min = Integer.MAX_VALUE;
for (int i = 0; i < n; i++) {
int[] sticker = stickers[i];
// 剪枝,贴纸包含第一个字符才处理,减少处理次数(只需要处理一次,没必要重复跑),贪心
if(sticker[chars[0] - 'a'] > 0) {
StringBuilder builder = new StringBuilder();
for (int j = 0; j < 26; j++) {
// 剩余字符转化的一维数组存在字符才处理
if(targetCounts[j] > 0) {
// 剩余的字符
int nums = targetCounts[j] - sticker[j];
for (int k = 0; k < nums; k++) {
builder.append((char)(j + 'a'));
}
}
}
String reset = builder.toString();
// 递归获取最小贴纸数
min = Math.min(min, process1(stickers, reset));
}
}
// 如果没有贴纸符合则返回最大integer, 否则最小贴纸数量加上当前字符数量
return min + (min == Integer.MAX_VALUE ? 0 : 1);
}
5 缓存(记忆化搜索)
直接添加缓存处理,因为处理的变量是字符串,用字符串变量没办法变成严格表结构的方式(空间不够)。故直接用缓存记忆化搜索即可
/**
* 递归处理贴纸(用二维数组优化版-剪枝)+ 缓存(记忆化搜索)
*
* @param stickers 所有的贴纸
* @param target 最终需要剪的值
* @return 最小贴纸数量
*/
public static int minStickers2(String[] stickers, String target) {
int n = stickers.length;
// 将贴纸转化为二维数组
int[][] counts = new int[n][26];
for (int i = 0; i < n; i++) {
char[] chars = stickers[i].toCharArray();
for (int i1 = 0; i1 < chars.length; i1++) {
counts[i][chars[i1] - 'a'] ++;
}
}
// 递归获取最小贴纸
HashMap<String, Integer> cache = new HashMap<>();
cache.put("", 0);
int ans = process2(counts, target,cache);
return ans == Integer.MAX_VALUE ? -1 : ans;
}
/**
* 贴纸优化版本
*
* @param stickers 二维数组处理贴纸
* @param target 剩余需要匹配的字符
* @return 最小贴纸数量
*/
private static int process2(int[][] stickers, String target, HashMap<String, Integer> cache) {
if(cache.containsKey(target)) {
return cache.get(target);
}
if(target.length() == 0) {
return 0;
}
// 用一维数组转化target
char[] chars = target.toCharArray();
int[] targetCounts = new int[26];
for (char aChar : chars) {
targetCounts[aChar - 'a']++;
}
int n = stickers.length;
int min = Integer.MAX_VALUE;
for (int i = 0; i < n; i++) {
int[] sticker = stickers[i];
// 剪枝,贴纸包含第一个字符才处理,减少处理次数
if(sticker[chars[0] - 'a'] > 0) {
StringBuilder builder = new StringBuilder();
for (int j = 0; j < 26; j++) {
// 剩余字符转化的一维数组存在字符才处理
if(targetCounts[j] > 0) {
// 剩余的字符
int nums = targetCounts[j] - sticker[j];
for (int k = 0; k < nums; k++) {
builder.append((char)(j + 'a'));
}
}
}
String reset = builder.toString();
// 递归获取最小贴纸数
min = Math.min(min, process2(stickers, reset, cache));
}
}
// 如果没有贴纸符合则返回最大integer, 否则最小贴纸数量加上当前字符数量
int ans = min + (min == Integer.MAX_VALUE ? 0 : 1);
cache.put(target, ans);
return ans;
}
七、获取最长公共子序列
0 模型汇总
总结模型:一、从左往右尝试模型(机器人)。二、范围尝试模型(纸牌游戏)。三、样本对应模型(当前题)。四、业务限制模型
1 题目
给定两个字符串str1和str2,返回这两个字符串的最长公共子序列长度
比如 : str1 = “a12b3c456d”,str2 = “1ef23ghi4j56k”最长公共子序列是“123456”,所以返回长度6
2 思路
1、只关心0~i, 0~j的最长公共子序列
2、如果i第一个字符串只有一个字符
- 这个字符和第二个字符串的最后一个字符相等则返回1
- 否则递归获取第一个字符j-1的最长公共子序列
3、如果j第一个字符串只有一个字符
- 这个字符和第二个字符串的最后一个字符相等则返回1
- 否则递归获取第一个字符i-1的最长公共子序列
4、其他情况,样本对应(一般都是看两个样本的最后一个字符)
- 不考虑i位置以公共子序列结尾,可能考虑j位置以公共子序列结尾
- 不考虑j位置以公共子序列结尾,可能考虑i位置以公共子序列结尾
- 就以i和j位置以公共子序列结尾
3 递归
public static int longestCommonSubsequence(String s1, String s2) {
if(s1 == null || s1.isEmpty() || s2 == null || s2.isEmpty()) {
return 0;
}
return process(s1.toCharArray(), s2.toCharArray(), s1.length() - 1, s2.length() - 1);
}
private static int process(char[] str1, char[] str2, int i, int j) {
if(i == 0 && j== 0) {
return str1[i] == str2[j] ? 1 : 0;
}
// 第一个样本只有1个字符
else if(i == 0) {
// 这个字符和第二个字符串的最后一个字符相等则返回1
if(str1[i] == str2[j]) {
return 1;
} else {
// 否则递归获取第一个字符j-1的最长公共子序列
return process(str1, str2, i, j - 1);
}
}
// 第二个样本只有一个字符
else if(j == 0) {
if(str1[i] == str2[j]) {
return 1;
} else {
return process(str1, str2, i - 1, j);
}
} else {
// 不考虑i位置以公共子序列结尾,可能考虑j位置以公共子序列结尾
int p1 = process(str1, str2, i - 1, j);
// 不考虑j位置以公共子序列结尾,可能考虑i位置以公共子序列结尾
int p2 = process(str1, str2, i, j - 1);
// 就以i和j位置以公共子序列结尾
int p3 = str1[i] == str2[j] ? (1 + process(str1, str2, i - 1, j -1)) : 0;
return Math.max(p1, Math.max(p2, p3));
}
}
4 动态规划
1、分析可变参数是i和j是样本的长度则可以用二维数组就可以容纳所有的值
2、可变参数的变化范围是i-1,j-1,j-1和i-1。则只要通过基础条件先赋值0行和0列的值就可以用递归的结构填充动态规划的值
3、基础条件直接转化即可
/**
* 动态规划找到最大公共子序列
*
* @param s1 字符串a
* @param s2 字符串b
* @return
*/
public static int longestCommonSubsequence1(String s1, String s2) {
if (s1 == null || s1.isEmpty() || s2 == null || s2.isEmpty()) {
return 0;
}
// 创建动态规划表
char[] str1 = s1.toCharArray();
char[] str2 = s2.toCharArray();
int n = str1.length;
int m = str2.length;
int[][] dp = new int[n][m];
// 通过递归直接计算第一个值
dp[0][0] = str1[0] == str2[0] ? 1 : 0;
// 从下标1开始计算i的值(列)
for (int i = 1; i < n; i++) {
dp[i][0] = str1[i]== str2[0] ? 1 : dp[i -1][0];
}
// 从下标1开始计算j的值(行)
for (int j = 1; j < m; j++) {
dp[0][j] = str1[0]== str2[j] ? 1 : dp[0][j -1];
}
// 计算其他情况
for (int i = 1; i < n; i++) {
for (int j = 1; j < m; j++) {
// 不考虑i位置以公共子序列结尾,可能考虑j位置以公共子序列结尾
int p1 = dp[i - 1][j];
// 不考虑j位置以公共子序列结尾,可能考虑i位置以公共子序列结尾
int p2 = dp[i][j - 1];
// 就以i和j位置以公共子序列结尾
int p3 = str1[i] == str2[j] ? (1 + dp[i - 1][j -1]) : 0;
dp[i][j] = Math.max(p1, Math.max(p2, p3));
}
}
return dp[n-1][m-1];
}
八、最长回文子序列的长度
1 题目
给定一个字符串str,返回这个字符串的最长回文子序列长度
比如 : str = “a12b3c43def2ghi1kpm”最长回文子序列是“1234321”或者“123c321”,返回长度7
2 思路
样本对应方式:
1、先生成一个逆序串
2、获取原字符和逆序串的最长子序列,两个字符串的公共子序列就是最长回文子序列
范围尝试模型(经验:特别注重开头和结尾):
1、利用递归处理L~R的最长公共子序列
2、只有一个字符:(一个字符就是回文),则返回1
3、两个字符:两个字符相等则是2个回文,否则是1个回文
4、多个字符则获取每种情况的结果的最大值(max)
- 不已L结尾,也不已R结尾。两个都不要,直接往中间走 L + 1, R - 1
- 已L结尾,不已R结尾.。则R往前走 L , R - 1
- 不已L结尾,已R结尾。则L往前走L + 1, R
- 已L结尾,也已R结尾。两个字符相等才存在回文,则 { L + 1, R - 1} + 2
3 递归
public static int longestPalindromeSubseq(String str) {
if(str == null || str.isEmpty()) {
return 0;
}
return process(str.toCharArray(), 0, str.length() - 1);
}
private static int process(char[] chars, int l, int r){
// 只有一个字符:(一个字符就是回文),则返回1
if(l == r) {
return 1;
}
// 两个字符:两个字符相等则是回文,否则不是
if(l == r - 1) {
return chars[l] == chars[r] ? 2 : 1;
}
// 多个字符则获取每种情况的结果的最大值(max)
// 不已L结尾,也不已R结尾。两个都不要,直接往中间走 L + 1, R - 1
int p1 = process(chars, l + 1, r - 1);
// 已L结尾,不已R结尾.。则R往前走 L , R - 1
int p2 = process(chars, l, r - 1);
// 不已L结尾,已R结尾。则L往前走L + 1, R
int p3 = process(chars, l + 1, r);
// 已L结尾,也已R结尾。两个字符相等才存在回文,2是两个数都要
int p4 = chars[l] != chars[r] ? 0 : 2 + process(chars, l + 1, r - 1);
return Math.max(p1, Math.max(p2, Math.max(p3, p4)));
}
4 动态规划
1、可变参数就是L和R,用dp=new int[n][n]
2、L>R是不可能出现的
3、根据base case, L=R时赋值为1
4、根据base case, L=R-1也直接赋值
5、根据递归得出只需要左、左下、左的值就可以计算出所有的值
public static int dp(String str) {
if(str == null || str.isEmpty()) {
return 0;
}
char[] chars = str.toCharArray();
int n = chars.length;
int[][] dp = new int[n][n];
// 先将最后一个位置赋值为1
dp[n - 1][n - 1] = 1;
// 遍历到n - 1的前一个位置
for (int i = 0; i < n - 1; i++) {
dp[i][i] = 1;
dp[i][i + 1] = chars[i] == chars[i + 1] ? 2 : 1;
}
// l的前两位已经赋值了,则从后面第三个开始
for (int l = n - 3; l >= 0; l--) {
// 从l往后2个位置开始遍历
for (int r = l + 2; r < n ; r++) {
// 不已L结尾,也不已R结尾。两个都不要,直接往中间走 L + 1, R - 1
int p1 = dp[l + 1][r - 1];
// 已L结尾,不已R结尾.。则R往前走 L , R - 1
int p2 = dp[l][r - 1];
// 不已L结尾,已R结尾。则L往前走L + 1, R
int p3 = dp[l + 1][r];
// 已L结尾,也已R结尾。两个字符相等才存在回文,2是两个数都要
int p4 = chars[l] != chars[r] ? 0 : (2 + dp[l + 1][r - 1]);
dp[l][r] = Math.max(p1, Math.max(p2, Math.max(p3, p4)));
}
}
return dp[0][n - 1];
}
5 动态规划优化
格子的值依赖左、下、左下。 则得出结论
1、格子的值绝不会比左下、左、下的值小
2、则可能性左下可以删掉,只需要左、下和第四种可能性
public static int dp1(String str) {
if(str == null || str.isEmpty()) {
return 0;
}
char[] chars = str.toCharArray();
int n = chars.length;
int[][] dp = new int[n][n];
// 先将最后一个位置赋值为1
dp[n - 1][n - 1] = 1;
// 遍历到n - 1的前一个位置
for (int i = 0; i < n - 1; i++) {
dp[i][i] = 1;
dp[i][i + 1] = chars[i] == chars[i + 1] ? 2 : 1;
}
// l的前两位已经赋值了,则从后面第三个开始
for (int l = n - 3; l >= 0; l--) {
// 从l往后2个位置开始遍历
for (int r = l + 2; r < n ; r++) {
// 已L结尾,不已R结尾.。则R往前走 L , R - 1
int p2 = dp[l][r - 1];
// 不已L结尾,已R结尾。则L往前走L + 1, R
int p3 = dp[l + 1][r];
dp[l][r] = Math.max(p2, p3);
if(chars[l] == chars[r]) {
dp[l][r] = Math.max(dp[l][r], (2 + dp[l + 1][r - 1]));
}
}
}
return dp[0][n - 1];
九、象棋马k步的方法数
1 题目
自行搜索或者想象一个象棋的棋盘,然后把整个棋盘放入第一象限,棋盘的最左下角是(0,0)位置那么整个棋盘就是横坐标上9条线、纵坐标上10条线的区域
给你三个 参数 x,y,k返回“马”从(0,0)位置出发,必须走k步最后落在(x,y)上的方法数有多少种?
2 思路
1、越界base cace
2、步数为0的时候,如果当前位置是给定的位置则存在一种方法,否则没有
3、马跳存在8种方法,每种方法都尝试后汇总数量就是所有的方法数
3 递归尝试
public static int jump(int x, int y, int k) {
return process(0, 0, k, x, y);
}
/**
* 递归获取马跳到目标格子的所有情况
*
* 棋盘横9纵10
*
* @param a 开始的x位置
* @param b 开始的y位置
* @param rest 剩余跳的步数
* @param x 目标的x位置
* @param y 目标的y位置
* @return 所有的情况
*/
private static int process(int a, int b, int rest, int x, int y) {
if(a < 0 || b < 0 || a > 9 || b > 8) {
return 0;
}
// 步数结束到达目标位置则存在一种方法
if(rest == 0) {
return (a == x && b == y) ? 1 : 0;
}
// 格子跳有8种情况汇总就是所有的情况
int ways = process(a + 2, b + 1, rest - 1, x, y);
ways += process(a + 1, b + 2, rest - 1, x, y);
ways += process(a - 1, b + 2, rest - 1, x, y);
ways += process(a - 2, b + 1, rest - 1, x, y);
ways += process(a - 2, b - 1, rest - 1, x, y);
ways += process(a - 1, b - 2, rest - 1, x, y);
ways += process(a + 1, b - 2, rest - 1, x, y);
ways += process(a + 2, b - 1, rest - 1, x, y);
return ways;
}
4 动态规划
1、分析递归的可变参数有3个,x、y、k则dp表为三位数组
2、八种方式每种方式都是k-1, 则当前层都依赖下一层
3、最下一层的k=0的值为1其他值i为0,则从下往上获取值
4、由递归得知边界值不符合返回数量为0,则利用pick函数处理
/**
* 动态规划获取马的跳转步数
*
* @param x x目标位置
* @param y y目标位置
* @param k 能跳的步数
* @return 所有能跳过去的总情况数
*/
public static int dp(int x, int y, int k) {
int[][][] dp = new int[10][9][k + 1];
// 步数结束到达目标位置则存在一种方法
dp[x][y][0] = 1;
// 遍历步数,从1开始,0已经赋值了
for (int rest = 1; rest <= k; rest++) {
// 从左往右处理x值
for (int a = 0; a < 10; a++) {
// 从左往右处理y值
for (int b = 0; b < 9; b++) {
int ways = pick(dp, a + 2, b + 1, rest - 1);
ways += pick(dp,a + 1, b + 2, rest - 1);
ways += pick(dp,a - 1, b + 2, rest - 1);
ways += pick(dp,a - 2, b + 1, rest - 1);
ways += pick(dp,a - 2, b - 1, rest - 1);
ways += pick(dp,a - 1, b - 2, rest - 1);
ways += pick(dp,a + 1, b - 2, rest - 1);
ways += pick(dp,a + 2, b - 1, rest - 1);
dp[a][b][rest] = ways;
}
}
}
return dp[0][0][k];
}
/**
* 获取参数值,如果超出边界则返回0
*/
private static int pick(int[][][] dp, int a, int b, int k) {
// 边界值处理
if(a < 0 || b < 0 || a > 9 || b > 8) {
return 0;
}
return dp[a][b][k];
}
十、咖啡机做咖啡后杯子最短干净时间
1 题目
给定一个数组arr,arr[i]代表第i号咖啡机泡一杯咖啡的时间。给定一个正数N,表示N个人等着咖啡机泡咖啡,每台咖啡机只能轮流泡咖啡。
只有一台洗咖啡杯机,一次只能洗一个杯子,时间耗费a,洗完才能洗下一杯。每个咖啡杯也可以自己挥发干净,时间耗费b,咖啡杯可以并行挥发
假设所有人拿到咖啡之后立刻喝干净,返回从开始等到所有咖啡机变干净的最短时间三个参数:int[] arr、int N,int a、int b
2 思路
1、第一步:利用小根堆给每个人做咖啡,获取所有人喝咖啡的列表
2、第二步:递归去洗杯子
- 用洗咖啡机去洗:1、洗咖啡机时间空闲了当前杯子可能没到时间,当前杯子到时间了咖啡机可能不空闲,去最大即可。2、当前杯子洗之后的时间就是下一个杯子洗咖啡机的剩余时间
- 挥发:1、并行直接加洗咖啡杯的时间。2、洗咖啡机时间不变
3 递归尝试
/**
* 获取最小咖啡杯变干净的时间
*
* @param arr 第i号机器泡咖啡的时间
* @param n n个人等待泡咖啡
* @param a 洗咖啡机耗时
* @param b 咖啡杯自己挥发耗时
* @return 最小咖啡杯变干净的时间
*/
public static int minTime(int[] arr, int n, int a, int b) {
// 利用大根堆做咖啡
PriorityQueue<Machine> queue = new PriorityQueue<>((f, t) ->
(f.timePoint + f.workTime) - (t.timePoint + t.workTime));
// 初始化机器的时间和工作时间
for (int i = 0; i < arr.length; i++) {
queue.add(new Machine(0, arr[i]));
}
// n个人的喝完时间, 获取喝完最优数组(最优排对)
int[] drink = new int[n];
for (int i = 0; i < n; i++) {
Machine poll = queue.poll();
// 工作时间往后加
poll.timePoint += poll.workTime;
// 喝完的时间放入drink
drink[i] = poll.timePoint;
queue.add(poll);
}
// 从下标0开始,时间为0
return bestTime(drink, a, b, 0, 0);
}
/**
* 最好洗杯子时间
*
* @param drink n个人的喝完时间(可以开始洗的时间)
* @param a 洗咖啡机耗时(串行)
* @param b 咖啡杯自己挥发耗时(并行)
* @param index 当前人数下标
* @param free 洗咖啡机可用时间
* @return 所有杯子都变干净的最早结束时间
*/
private static int bestTime(int[] drink, int a, int b, int index, int free) {
// 洗完了
if(index == drink.length){
return 0;
}
// index号杯子决定洗
// 开始洗的时间和洗咖啡可用时间的最大时间 + 洗咖啡耗时(喝完后洗咖啡杯机器可能不空闲,咖啡机空闲但是开始洗的时间大)
int selfClean = Math.max(drink[index], free) + a;
int restClean = bestTime(drink, a, b, index + 1, selfClean);
// 木桶原理(当前的时间和后面的其他杯子的时间选最大)
int p1 = Math.max(selfClean, restClean);
// index号杯子决定挥发
// 喝完后就挥发(并行)
int selfClean1 = drink[index] + b;
int restClean1 = bestTime(drink, a, b, index + 1, free);
// 木桶原理(当前的时间和后面的其他杯子的时间选最大)
int p2 = Math.max(selfClean1, restClean1);
// 获取最小的方案
return Math.min(p1, p2);
}
// 机器
public static class Machine{
// 当前时间点
public int timePoint;
// 做一杯咖啡的时间
public int workTime;
public Machine(int timePoint, int workTime) {
this.timePoint = timePoint;
this.workTime = workTime;
}
}
4 动态规划
1、可变参数是两个,分析可以用二维表作为动态规划表
2、free参数不能直观的得到变化范围,就是业务限制模型(人为想限制,限制不够业务来凑)。
- 计算最大的洗咖啡杯时间,作为dp表大小值
- 从下往上计算,(都依赖后面的值)
3、根据递归的逻辑改为dp动态规划即可
- 大于最大洗咖啡杯时间则不进行计算(解决越界问题)
/**
* 获取最小咖啡杯变干净的时间
*
* @param arr 第i号机器泡咖啡的时间
* @param n n个人等待泡咖啡
* @param a 洗咖啡机耗时
* @param b 咖啡杯自己挥发耗时
* @return 最小咖啡杯变干净的时间
*/
public static int minTime1(int[] arr, int n, int a, int b) {
// 利用大根堆做咖啡
PriorityQueue<Machine> queue = new PriorityQueue<>((f, t) ->
(f.timePoint + f.workTime) - (t.timePoint + t.workTime));
// 初始化机器的时间和工作时间
for (int i = 0; i < arr.length; i++) {
queue.add(new Machine(0, arr[i]));
}
// n个人的喝完时间, 获取喝完最优数组(最优排对)
int[] drink = new int[n];
for (int i = 0; i < n; i++) {
Machine poll = queue.poll();
// 工作时间往后加
poll.timePoint += poll.workTime;
// 喝完的时间放入drink
drink[i] = poll.timePoint;
queue.add(poll);
}
// 从下标0开始,时间为0
return dp(drink, a, b);
}
/**
* 动态规划最好洗杯子时间
*
* @param drink n个人的喝完时间(可以开始洗的时间)
* @param a 洗咖啡机耗时(串行)
* @param b 咖啡杯自己挥发耗时(并行)
* @return 所有杯子都变干净的最早结束时间
*/
private static int dp(int[] drink, int a, int b) {
int n = drink.length;
int maxFree = 0;
for (int i = 0; i < drink.length; i++) {
maxFree = Math.max(drink[i], maxFree) + a;
}
int[][] dp = new int[n + 1][maxFree + 1];
for (int index = n - 1; index >= 0 ; index--) {
for (int free = 0; free <= maxFree; free++) {
// index号杯子决定洗
// 开始洗的时间和洗咖啡可用时间的最大时间 + 洗咖啡耗时(喝完后洗咖啡杯机器可能不空闲,咖啡机空闲但是开始洗的时间大)
int selfClean = Math.max(drink[index], free) + a;
if(selfClean > maxFree) {
continue;
}
int restClean = dp[index + 1][selfClean];
// 木桶原理(当前的时间和后面的其他杯子的时间选最大)
int p1 = Math.max(selfClean, restClean);
// index号杯子决定挥发
// 喝完后就挥发(并行)
int selfClean1 = drink[index] + b;
int restClean1 = dp[index + 1][free];
// 木桶原理(当前的时间和后面的其他杯子的时间选最大)
int p2 = Math.max(selfClean1, restClean1);
// 获取最小的方案
dp[index][free] = Math.min(p1, p2);
}
}
return dp[0][0];
}
十一、返回二维数组最小距离累加和
1 题目
给定一个二维数组matrix,一个人必须从左上角出发,最后到达右下角沿途只可以向下或者向右走,沿途的数字都累加就是距离累加和返回最小距离累加和
2 思路
经典dp方案:
1、这个人只有两种尝试的办法,往下走或者往右走
2、通过二维数组建立dp表
- 第一行只能从左往右记录累加和
- 第一列只能从上往下记录累加和
- 其他位置,依赖左边和上边的值,谁小选择谁。值等于当前值+小的格子的值
3、返回最后面格子的值
优化思路(省空间)【数据压缩】:
1、只需要当前行和上面一行的值就足以计算结果,不用把整张dp表都计算出来
2、只创建两个数组,用于记录上一行和当前行的数据,计算到最后一行取值即可
3、继续优化,可以只用一个数组进行计算:计算后放入当前位置,计算下一个位置的值,一直循环
3 动态规划
// dp动态规划+计算整张dp表
public static int minPathSum(int[][] m) {
if(m == null || m.length == 0 || m[0] == null || m[0].length == 0) {
return 0;
}
int row = m.length;
int col = m[0].length;
int[][] dp = new int[row][col];
dp[0][0] = m[0][0];
// 先填第一行
for (int i = 1; i < row; i++) {
dp[i][0] = dp[i - 1][0] + m[i][0];
}
// 在填第一列
for (int i = 1; i < col; i++) {
dp[0][i] = dp[0][i - 1] + m[0][i];
}
// 其他数据获取左边和上面小的值
for (int i = 1; i < row; i++) {
for (int j = 1; j < col; j++) {
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + m[i][j];
}
}
return dp[row - 1][col - 1];
}
4 动态规划(空间压缩)
// dp动态规划 + 空间压缩(只计算一个数组)
public static int minPathSum1(int[][] m) {
if (m == null || m.length == 0 || m[0] == null || m[0].length == 0) {
return 0;
}
int row = m.length;
int col = m[0].length;
int[] arr = new int[col];
arr[0] = m[0][0];
// 初始化第一列
for (int i = 1; i < col; i++) {
arr[i] = arr[i - 1] + m[0][i];
}
for (int i = 1; i < row; i++) {
// 先计算出第一行下标为0的值
arr[0] += m[i][0];
for (int j = 1; j < col; j++) {
// 当前j下标前一个就是当前值左边的值,当前位置的值就是上面的值
// 取左边和上边最小的值 + 当前位置的值
arr[j] = Math.min(arr[j - 1], arr[j]) + m[i][j];
}
}
return arr[col - 1];
}
总结:空间压缩技巧,更近一步压缩空间。上、左用一个数组计算。左、左上、上添加一个变量也可以用一个数组进行计算。如果行的数量多就用列压缩,列的数量多就用行压缩。
十二、返回组成aim的方法数(货币数组)
1 题目
arr是货币数组,其中的值都是正数。再给定一个正数aim。
每个值都认为是一张货币,即便是值相同的货币也认为每一张都是不同的,返回组成aim的方法数
例如:arr = {1,1,1},aim = 2第0个和第1个能组成2,第1个和第2个能组成2,第0个和第2个能组成2一共就3种方法,所以返回3
2 思路
从左往后模型
1、递归处理如果目标钱为0则结束流程
2、如果index处理完了,目标刚好为0则存在一种方法
3、否则累加要当前值和不要当前的方法数就是最多的方法数
3 递归尝试
public static int coinWays(int[] arr, int aim) {
return process(arr, 0, aim);
}
private static int process(int[] arr, int index, int rest) {
if(rest < 0) {
return 0;
}
// 数组匹配完
if(index == arr.length) {
// 刚好达到目标则方法数为1,否则为0
return rest == 0 ? 1 : 0;
}
// 不要index的钱 + 要index的钱
return process(arr, index + 1, rest) + process(arr, index + 1, rest - arr[index]);
}
4 动态规划
1、分析可变参数是index和rest,用二维数组即可完成
2、index都依赖jindex+1的值,则从后往前遍历
3、处理一下越界问题即可
public static int dp(int[] arr, int aim) {
if(aim == 0) {
return 1;
}
int n = arr.length;
int[][] dp = new int[n + 1][aim + 1];
// index=n时,rest=0时等于1
dp[n][0] = 1;
// index都依赖jindex+1的值,则从后往前遍历
for (int index = n - 1; index >= 0; index--) {
for (int rest = 0; rest <= aim; rest++) {
dp[index][rest] =
// 不要当前值
dp[index + 1][rest]
// 要当前值,判断是否越界,越界则返回0
+ (rest - arr[index] >= 0 ? dp[index + 1][rest - arr[index]] : 0);
}
}
return dp[0][aim];
}
十三、返回组成aim的方法数(面值数组)
1 题目
arr是面值数组,其中的值都是正数且没有重复。再给定一个正数aim。
每个值都认为是一种面值,且认为张数是无限的。返回组成aim的方法数
例如:arr = {1,2},aim = 4方法如下:1+1+1+1、1+1+2、2+2一共就3种方法,所以返回3
2 思路
1、递归处理如果目标钱为0则结束流程
2、遍历张数从0张开始,一直累加张数往后遍历,获取每种情况的总方法数返回
3 递归
public static int coinWays(int[] arr, int aim) {
return process(arr, 0, aim);
}
/**
* 获取index下标的面值组成方法数据
*
* @param arr 面值数组
* @param index 当前处理值
* @param rest 剩余金额
* @return 所有组成方法数
*/
private static int process(int[] arr, int index, int rest) {
// 到了最后一个下标(没钱了)
if(index == arr.length) {
// 刚好达到目标则存在一种方法数
return rest == 0 ? 1 : 0;
}
int ways = 0;
// 当前要0张~(张数*当前面值<=剩余金额)
for (int zhang = 0; zhang * arr[index] <= rest; zhang++) {
// 递归获取后面的所有情况,并进行累加
ways += process(arr, index + 1, rest - (zhang * arr[index]));
}
return ways;
}
4 动态规划
1、分析可变参数为2个,则使用二维数组作为dp表
2、将递归方式改为动态规划方法
/**
* 动态规划处理面值计算
*
* @param arr 所有的面值
* @param aim 需要计算的金额
* @return 所有的方法数
*/
public static int dp(int[] arr, int aim) {
if (arr == null || arr.length == 0 || aim < 0) {
return 0;
}
int n = arr.length;
int[][] dp = new int[n + 1][aim + 1];
dp[n][0] = 1;
for (int index = n - 1; index >= 0 ; index--) {
for (int rest = 0; rest <= aim; rest++) {
int ways = 0;
for (int zhang = 0; zhang * arr[index] <= rest; zhang++) {
// 递归获取后面的所有情况,并进行累加
ways += dp[index + 1][rest - (zhang * arr[index])];
}
dp[index][rest] = ways;
}
}
return dp[0][aim];
}
当前动态规划里面多了一个for循环,计算一个格子需要一个for循环。
5 记忆化搜索和动态规划总结
递归:所有情况都走,有重复计算(暴力所有过程)
记忆化搜索:将重复计算缓存起来,
动态规划(严格表结构):严格整理好依赖关系,从简单位置计算到复杂位置直到将所有位置计算出来。(表多大复杂度就多大)
如果单个计算没有枚举行为(for循环),记忆化搜索和严格表结构的方式相同。有枚举行为则优化为严格表结构之后继续优化(建立空间感后分析优化方案)
上面的动态建立dp表之后,通过观察得知 > 当前格子需要遍历获取下一层的所有累加和 > 下一层的累加和就是当前格子左边的值 > 则得出结论:当前格子的值通过下边和左边格子的值就能计算出当前格子的值(减掉了for循环)
/**
* 动态规划处理面值计算(通过观察继续优化减掉for循环)
*
* @param arr 所有的面值
* @param aim 需要计算的金额
* @return 所有的方法数
*/
public static int dp1(int[] arr, int aim) {
if (arr == null || arr.length == 0 || aim < 0) {
return 0;
}
int n = arr.length;
int[][] dp = new int[n + 1][aim + 1];
dp[n][0] = 1;
for (int index = n - 1; index >= 0 ; index--) {
for (int rest = 0; rest <= aim; rest++) {
// 获取下一个格子的值
dp[index][rest] = dp[index + 1][rest];
// 如果当前左边格子的值>=0
if(rest - arr[index] >= 0) {
// 则加上左边格子的值
dp[index][rest] += dp[index][rest - arr[index]];
}
}
}
return dp[0][aim];
}
十四、返回组成aim的方法数(货币数组)
1 题目
arr是货币数组,其中的值都是正数。再给定一个正数aim。每个值都认为是一张货币,认为值相同的货币没有任何不同,返回组成aim的方法数
例如:arr = {1,2,1,1,2,1,2},aim = 4方法:1+1+1+1、1+1+2、2+2一共就3种方法,所以返回3
2 递归
// 主函数:从0开始往后递归处理的所有方法数就是所有方法数
public static int coinsWay(int[] arr, int aim) {
if (arr == null || arr.length == 0 || aim < 0) {
return 0;
}
Info info = getInfo(arr);
return process(info.coins, info.nums, 0, aim);
}
/**
* 获取最多方法数
*
* @param coins 面值数组
* @param nums 数量数组
* @param i 当前处理位置
* @param rest 剩余金额
* @return 方法数
*/
private static int process(int[] coins, int[] nums, int i, int rest) {
if(i == coins.length) {
return rest == 0 ? 1 : 0;
}
int ways = 0;
// 面值小于等于剩余金额 与 张数小于等于总张数
for (int zhang = 0; zhang * coins[i] <= rest && zhang <= nums[i]; zhang++) {
// 递归处理下一张面值
ways += process(coins, nums, i + 1, rest - (zhang * coins[i]));
}
return ways;
}
// 通过面值获取info数据
private static Info getInfo(int[] arr) {
// 将相同面值的统计出现的次数
HashMap<Integer, Integer> counts = new HashMap<>();
for (int i : arr) {
if(counts.containsKey(i)) {
counts.put(i, 1);
} else {
counts.put(i, counts.get(i) + 1);
}
}
// 将面额放入coins,张数放入nums
int n = counts.size();
int[] coins = new int[n];
int[] nums = new int[n];
int index = 0;
for (Map.Entry<Integer, Integer> entry : counts.entrySet()) {
coins[index] = entry.getKey();
nums[index++] = entry.getValue();
}
return new Info(coins, nums);
}
/**
* 动态规划处理
*
* @param arr 面值数据
* @param aim 目标金额
* @return 总数量
*/
public static int dp(int[] arr, int aim) {
return 0;
}
private static class Info{
// 面值数组
private int[] coins;
// 面值张数数组
private int[] nums;
public Info(int[] coins, int[] nums) {
this.coins = coins;
this.nums = nums;
}
}
3 动态规划
/**
* 动态规划处理
*
* @param arr 面值数据
* @param aim 目标金额
* @return 总数量
*/
public static int dp(int[] arr, int aim) {
if (arr == null || arr.length == 0 || aim < 0) {
return 0;
}
Info info = getInfo(arr);
int[] coins = info.coins;
int[] nums = info.nums;
int n = nums.length;
int[][] dp = new int[n + 1][aim + 1];
dp[n][0] = 1;
for (int index = n - 1; index >= 0; index--) {
for (int rest = 0; rest <= aim; rest++) {
int ways = 0;
// 面值小于等于剩余金额 与 张数小于等于总张数
for (int zhang = 0; zhang * coins[index] <= rest && zhang <= nums[index]; zhang++) {
// 递归处理下一张面值
ways += dp[index + 1][rest - (zhang * coins[index])];
}
dp[index][rest] = ways;
}
}
return dp[0][aim];
}
4 动态规划优化(空间压缩)
1、分析数据可以将动态规划里面的for循环优化掉
2、循环中会出现重复值,减掉即可
/**
* 动态规划处理(优化处理)空间压缩
*
* @param arr 面值数据
* @param aim 目标金额
* @return 总数量
*/
public static int dp1(int[] arr, int aim) {
if (arr == null || arr.length == 0 || aim < 0) {
return 0;
}
Info info = getInfo(arr);
int[] coins = info.coins;
int[] nums = info.nums;
int n = nums.length;
int[][] dp = new int[n + 1][aim + 1];
dp[n][0] = 1;
for (int index = n - 1; index >= 0; index--) {
for (int rest = 0; rest <= aim; rest++) {
dp[index][rest] = dp[index + 1][rest];
// 未越界
if(rest - coins[index] >= 0) {
dp[index][rest] += dp[index][rest - coins[index]];
}
// 判断是否存在重复值,存在则减掉
if(rest - coins[index] * (nums[index] + 1) >= 0) {
dp[index][rest] -= dp[index + 1][rest - coins[index] * (nums[index] + 1)];
}
}
}
return dp[0][aim];
}
十五、返回k步之后Bob活着的概率
1 题目
给定5个参数,N,M,row,col,k表示在N*M的区域上,醉汉Bob初始在(row,col)位置。Bob一共要迈出k步,且每步都会等概率向上下左右四个方向走一个单位。
任何时候Bob只要离开NM的区域,就直接死亡。返回k步之后,Bob还在NM的区域的概率
2 思路
1、概率就是 获取所有的生存情况除以所有会发生的情况(4的k次方)就是答案
2、获取所有生成情况的方式和第九题象棋跳马问题一样
3 递归
/**
* 获取醉汉的生存概率
*
* @param row 区域的行
* @param col 区域的列
* @param k 走k步
* @param n 当前的行位置
* @param k 当前的列位置
* @return 生存概率
*/
public static double liveProbability(int row, int col, int k, int n, int m){
return (double)process(row, col, k, n, m) / Math.pow(4, k);
}
/**
* 获取醉汉的所有生存情况
*
* @param row 区域的行
* @param col 区域的列
* @param rest 剩余的步数
* @param n 当前的行位置
* @param m 当前的列位置
* @return 生存总数
*/
private static int process(int row, int col, int rest, int n, int m) {
// 超出边界则死亡
if(row < 0 || row == n || col < 0 || col == m) {
return 0;
}
// 步数走完则生存
if(rest == 0) {
return 1;
}
// 上下左右的情况都走
int p1 = process(row, col, rest - 1, n - 1, m);
int p2 = process(row, col, rest - 1, n + 1, m);
int p3 = process(row, col, rest - 1, n, m - 1);
int p4 = process(row, col, rest - 1, n, m + 1);
return p1 + p2 + p3 + p4;
}
4 动态规划
和上面题目的动态规划一样,根据递归写出
/**
* 获取醉汉的生存概率
*
* @param row 区域的行
* @param col 区域的列
* @param k 走k步
* @param n 当前的行位置
* @param k 当前的列位置
* @return 生存概率
*/
public static double dp(int row, int col, int k, int n, int m){
int[][][] dp = new int[row][col][k + 1];
// 初始化位置k位置=0时,则生存
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
dp[i][j][0] = 1;
}
}
for (int rest = 1; rest < k=; rest++) {
for (int r = 0; r < row; r++) {
for (int c = 0; c < col; c++) {
// 计算上下左右的值累加上
dp[r][c][rest] = pick(dp, row, col, n + 1, m, rest - 1);
dp[r][c][rest] += pick(dp, row, col, n - 1, m, rest - 1);
dp[r][c][rest] += pick(dp, row, col, n, m + 1, rest - 1);
dp[r][c][rest] += pick(dp, row, col, n, m - 1, rest - 1);
}
}
}
// 计算概率返回
return (double)dp[n][m][k] / Math.pow(4, k);
}
// 超出位置则死亡,否则获取剩余步数的值
private static int pick(int[][][] dp, int row, int col, int n, int m, int rest) {
if(row < 0 || row == n || col < 0 || col == m) {
return 0;
}
return dp[n][m][rest];
}
十六、砍怪兽
1、题目
给定3个参数,N,M,K
怪兽有N滴血,等着英雄来砍自己英雄每一次打击,都会让怪兽流失[0~M]的血量。到底流失多少?每一次在[0~M]上等概率的获得一个值
求K次打击之后,英雄把怪兽砍死的概率
2、思路
样本对应模型
1、计算所有的情况m+1的k次方
2、0~m种的所有情况都遍历处理,直到k次处理完
3、血小于0则是则被砍死,累加所有砍死的情况数
/**
* 砍怪兽
*
* @param n 剩余的血
* @param m 每次的伤害0~m
* @param k 还有k次可以砍
* @return 返回砍死的概率
*/
public static double kill(int n, int m, int k) {
if(n < 1 || m < 1 || k < 1) {
return 0;
}
// 所有会出现的情况
long all = (long) Math.pow(m + 1, k);
long kill = execute(k, m, n);
return (double)kill / (double)all;
}
/**
* 砍怪兽
*
* @param times 还有*次可以砍
* @param m 每次的伤害0~m
* @param hp 剩余的血
* @return 砍死返回1
*/
private static long execute(int times, int m, int hp) {
if(times == 0) {
return hp <= 0 ? 1 : 0;
}
// 如果没有血了,后面的所有情况都是被砍死
if(hp <= 0) {
return (long) Math.pow(m + 1, times);
}
long ways = 0;
for (int i = 0; i <= m; i++) {
ways += execute(times - 1 , m, hp - i);
}
return ways;
}
3、动态规划
1、分析可变参数是times和hp,则可以衍生动态规划表
2、分析hp-i时可能出现负数,负数场景时再去砍怪兽所有情况都是砍死则m+1的k次方就是砍死次数,则添加判断提前规避
/**
* 动态规划
*
* @param n 剩余的血
* @param m 每次的伤害0~m
* @param k 还有k次可以砍
* @return 返回砍死的概率
*/
public static double dp(int n, int m, int k) {
if(n < 1 || m < 1 || k < 1) {
return 0;
}
// 所有会出现的情况
long all = (long) Math.pow(m + 1, k);
// 创建dp表
long[][] dp = new long[k + 1][n + 1];
// 只有0位置的值是1
dp[0][0] = 1;
for (int times = 1; times <= k; times++) {
// 如果没有血了,砍死数量就是后面的所有情况 (m + 1的times次方)
dp[times][0] = (long) Math.pow(m + 1, times);
for (int hp = 1; hp <= n; hp++) {
long ways = 0;
for (int i = 0; i <= m; i++) {
if(hp - i >= 0) {
ways += dp[times - 1 ][hp - i];
} else {
// 如果没有血了,砍死数量就是后面的所有情况
ways += (long)Math.pow(m + 1, times - 1);
}
}
dp[times][hp] = ways;
}
}
// 所有会出现的情况
long kill = dp[k][n];
return (double)kill / (double)all;
}
4、动态规划(空间压缩)
1、动态规划里面存在for循环,则分析规划表的上或者左的值是否可以使用(观察临近位置看是否能替掉枚举行为),寻找出规律
2、分析数据,比如m=0~3(每次可能掉的血),times=5(可以砍的刀数),hp=10(剩余的血)
- dp[times - 1][hp-i]: 掉0滴血时依赖dp[4][10]。(上一行...)
- dp[times - 1][hp-i]: 掉0滴血时依赖dp[4][9] ... 到dp[4][hp-i]
- 之后累加所有的值即可
3、则m=0~7时,dp[5][10] = dp[4][10~3],dp[5][11] = dp[4][11~4] 。可以得出: dp[5][11] = dp[5][10] + dp[4][11] - dp[4][3] 。减去的dp[4][3] 是由于dp[5][10] 里面多算的。
4、公式:dp[i][j-1] = dp[i-1][j-1 ~ [j-1-m],dp[i][j] = dp[i][j-1] + dp[i-1][j] - dp[i-1][ j - 1 - m]
5、如果拿不到格子也需要减掉Math.pow(m + 1, times - 1)
/**
* 动态规划(空间压缩)
*
* @param n 剩余的血
* @param m 每次的伤害0~m
* @param k 还有k次可以砍
* @return 返回砍死的概率
*/
public static double dp1(int n, int m, int k) {
if(n < 1 || m < 1 || k < 1) {
return 0;
}
// 所有会出现的情况
long all = (long) Math.pow(m + 1, k);
// 创建dp表
long[][] dp = new long[k + 1][n + 1];
// 只有0位置的值是1
dp[0][0] = 1;
for (int times = 1; times <= k; times++) {
// 如果没有血了,砍死数量就是后面的所有情况 (m + 1的times次方)
dp[times][0] = (long) Math.pow(m + 1, times);
for (int hp = 1; hp <= n; hp++) {
// 替换公式
dp[times][hp] = dp[times][hp -1] + dp[times - 1][hp];
// 拿到格子
if(hp - 1 - m >= 0) {
dp[times][hp] -= dp[times - 1][hp - 1 - m];
}
// 拿不到格子
else {
// 存在负数则也需要减掉
dp[times][hp] -= Math.pow(m + 1, times - 1);
}
}
}
// 所有会出现的情况
long kill = dp[k][n];
return (double)kill / (double)all;
}
十七、返回组成aim的最小方法数(面值张数无限)
1、题目
arr是面值数组,其中的值都是正数且没有重复。再给定一个正数aim。每个值都认为是一种面值,且认为张数是无限的。返回组成aim的最少货币数
2、思路
1、利用从左往右模型实现
2、所有的分支都尝试,获取最小的方法数
3、递归
/**
* 获取最小面值数量
*
* @param arr 所有的面值
* @param aim 目标金额
* @return 最小的面值数量
*/
public static int minCoins(int[] arr, int aim) {
return execute(arr, 0, aim);
}
/**
* 递归执行获取最小面值数量
*
* @param arr 所有的面值
* @param index 当前面值张数
* @param rest 剩余金额
* @return 最小面值
*/
private static int execute(int[] arr, int index, int rest){
// 最后一张
if(index == arr.length) {
// 没钱了则返回0张
return rest == 0 ? 0 : Integer.MAX_VALUE;
}
int ans = Integer.MAX_VALUE;
// 遍历张数 当前张数*面值<= 剩余金额
for (int zhang = 0; zhang * arr[index] <= rest; zhang++) {
// 递归处理后面的值
int next = execute(arr, index + 1, rest - zhang * arr[index]);
if(next != Integer.MAX_VALUE){
ans = Math.min(ans, next + zhang);
}
}
return ans;
}
4、动态规划
/**
* 获取最小面值数量
*
* @param arr 所有的面值
* @param aim 目标金额
* @return 最小的面值数量
*/
public static int dp(int[] arr, int aim) {
if(aim == 0) {
return 0;
}
int n = arr.length;
int[][] dp = new int[n + 1][aim + 1];
// 最后一张处理
for (int i = 1; i <= aim; i++) {
dp[n][i] = Integer.MAX_VALUE;
}
for (int index = n - 1; index >= 0 ; index--) {
for (int rest = 0; rest <= aim; rest++) {
int ans = Integer.MAX_VALUE;
// 遍历张数 当前张数*面值<= 剩余金额
for (int zhang = 0; zhang * arr[index] <= rest; zhang++) {
// 递归处理后面的值
int next = dp[index + 1][rest - zhang * arr[index]];
if(next != Integer.MAX_VALUE){
ans = Math.min(ans, next + zhang);
}
}
dp[index][rest] = ans;
}
}
return dp[0][aim];
}
4、动态规划(空间压缩)
1、分析枚举行为在获取当前值x时,是获取的的dp[index + 1][rest - zhang * arr[index]] + zhang 的所有张数情况的最小值
2、观察当前值的左边值y,发现左边的值已经求过值,则:x=min(y + 1, dp[index + 1][rest - zhang * arr[index]])
/**
* 获取最小面值数量
*
* @param arr 所有的面值
* @param aim 目标金额
* @return 最小的面值数量
*/
public static int dp1(int[] arr, int aim) {
if(aim == 0) {
return 0;
}
int n = arr.length;
int[][] dp = new int[n + 1][aim + 1];
// 最后一张处理
for (int i = 1; i <= aim; i++) {
dp[n][i] = Integer.MAX_VALUE;
}
for (int index = n - 1; index >= 0 ; index--) {
for (int rest = 0; rest <= aim; rest++) {
// 先赋值格子下面的值
dp[index][rest] = dp[index + 1][rest];
// 不越界
if(rest - arr[index] < 0){
continue;
}
// 过滤无效值
if(dp[index][rest - arr[index]] == Integer.MAX_VALUE) {
continue;
}
// 根据公式转化
dp[index][rest] = Math.min(dp[index][rest], dp[index][rest - arr[index]] + 1);
}
}
return dp[0][aim];
}
十八、求裂开方法数
1、题目
给定一个正数n,求n的裂开方法数,规定:后面的数不能比前面的数小
比如4的裂开方法有:1+1+1+1、1+1+2、1+3、2+2、45种,所以返回5
2、递归
public static int ways(int n) {
if(n < 0) {
return 0;
}
if(n == 1) {
return 1;
}
execute(1, n);
}
/**
* 递归拆分数字
*
* @param pre 上一个拆出来的数
* @param rest 剩余需要拆的数
* @return 返回拆解的方法数
*/
private static int execute(int pre, int rest) {
// 最后剩余0,则是一种有效的方法
if(rest == 0) {
return 1;
}
// 拆分的时候前面的数不能比后面的大
if (pre > rest) {
return 0;
}
// 等于就是存在一种有效方法
if(pre == rest) {
return 1;
}
int ways = 0;
for (int first = 0; first <= rest; first++) {
ways += execute(first, rest - first);
}
return ways;
}
3、动态规划
1、分析基础条件:rest的值都是1 。pre>rest的值都是0。rest-fist=0时值为1
2、可变参数以后两个pre和rest,用长度n的二维数组就可以
/**
* 动态规划获取拆分方式
*
* @param n 需要拆的数
* @return 拆分的方法数
*/
public static int dp(int n) {
if (n < 0) {
return 0;
}
// 等于就是存在一种有效方法
if(n == 1) {
return 1;
}
// 基础条件赋初始值
int[][] dp = new int[n+1][n+1];
for (int pre = 1; pre <= n; pre++) {
dp[pre][0] = 1;
dp[pre][pre] = 1;
}
// 遍历pre
for (int pre = n - 1; pre >= 1; pre--) {
// rest从pre往后一个开始(rest=pre已经填好了)
for (int rest = pre + 1; rest <=n ; rest++) {
int ways = 0;
for (int first = pre; first <= rest; first++) {
ways += dp[first][rest - first];
}
dp[pre][rest] = ways;
}
}
return dp[1][n];
}
4、动态规划(空间压缩)
观察动态规划得知(仔细观察),计算当前格子值则需要下格子和左边格子的值
/**
* 动态规划获取拆分方式(空间压缩)
*
* @param n 需要拆的数
* @return 拆分的方法数
*/
public static int dp1(int n) {
if (n < 0) {
return 0;
}
// 等于就是存在一种有效方法
if(n == 1) {
return 1;
}
// 基础条件赋初始值
int[][] dp = new int[n+1][n+1];
for (int pre = 1; pre <= n; pre++) {
dp[pre][0] = 1;
dp[pre][pre] = 1;
}
// 遍历pre
for (int pre = n - 1; pre >= 1; pre--) {
// rest从pre往后一个开始(rest=pre已经填好了)
for (int rest = pre + 1; rest <=n ; rest++) {
// 需要观察二维表找到优化空间
dp[pre][rest] = dp[pre + 1][rest];
dp[pre][rest] += dp[pre][rest -pre];
}
}
return dp[1][n];
}
十九、拆分数组返回最近的最小集合累加和(均匀)
1、题目
给定一个正数数组arr,请把arr中所有的数分成两个集合,尽量让两个集合的累加和接近返回:最接近的情况下,较小集合的累加和
2、思路
1、计算数组的累加和,计算累加和一半的值。之后找到最接近(小于等于)中间值的值。如果能找到相等的则拆分的相等,否则小于中间值的就是返回值
2、拆封的时候分为两种情况,一种是不要当前值,一种是要当前值(要当前值时需要考虑当前值是否大于中间值,如果大于则不要)
3、递归
public static int splitNum(int[] arr) {
if(arr == null || arr.length < 2) {
return 0;
}
int sum = 0;
for (int i : arr) {
sum += i;
}
return execute(arr, 0, sum / 2);
}
/**
* 递归找到离中间值最接近的值
*
* @param arr 原始数组
* @param index 当前处理到的下标
* @param rest 剩余的中点数
* @return 剩余的中点数
*/
private static int execute(int[] arr, int index, int rest) {
// 计算到最后了
if(index == arr.length) {
return 0;
}
// 第一种情况:不获取当前值
int p1 = execute(arr, index + 1, rest);
// 第二种情况: 使用当前值
int p2 = 0;
// 当前值小于中点数
if(arr[index] <= rest) {
p2 = arr[index] + execute(arr, index + 1, rest - arr[index]);
}
// 获取更接近中点的数
return Math.max(p1, p2);
}
4、动态规划
1、分析递归过程,发现有重复解,则可以用dp表进行优化
2、分析可变参数有两个,则一个二维表就可以存储。将递归直接转化为动态规划。
3、index的变化范围从0~n,rest的变化范围从0~sum/2
public static int dp(int[] arr) {
if(arr == null || arr.length < 2) {
return 0;
}
int sum = 0;
for (int i : arr) {
sum += i;
}
// 获取中间值
sum /= 2;
int n = arr.length;
int[][] dp = new int[n + 1][sum + 1];
for (int index = n - 1; index >= 0 ; index--) {
for (int rest = 0; rest <= sum; rest++) {
// 第一种情况:不获取当前值
int p1 = dp[index + 1][rest];
// 第二种情况: 使用当前值
int p2 = 0;
// 当前值小于中点数
if(arr[index] <= rest) {
p2 = arr[index] + dp[index + 1][rest - arr[index]];
}
// 获取更接近中点的数
dp[index][rest] = Math.max(p1, p2);
}
}
return dp[0][sum];
}
二十、拆分数组返回最近的最小集合累加和(要求数量)
1、题目
给定一个正数数组arr,请把arr中所有的数分成两个集合
如果arr长度为偶数,两个集合包含数的个数要一样多
如果arr长度为奇数,两个集合包含数的个数必须只差一个
请尽量让两个集合的累加和接近。返回:最接近的情况下,较小集合的累加和
2、思路
1、需要判断数组是奇数还是偶数个,偶数个则获取个数一半进行递归,奇数则获取中间值和前一个数的值去最大
2、递归时也分为两种情况,一种是不要当前值,一种是要当前值,要当前值则判断值是否有效,有效才获取值
3、递归
public static int splitSum(int[] arr) {
if(arr == null || arr.length < 2) {
return 0;
}
int sum = 0;
for (int i : arr) {
sum += i;
}
// 偶数
if((arr.length & 1) == 0) {
return execute(arr, 0, sum / 2, arr.length / 2);
}
// 奇数
return Math.max(execute(arr, 0, sum / 2, arr.length / 2),
execute(arr, 0, sum / 2, arr.length / 2 + 1));
}
/**
* 递归获取最接近中间数的累加和
*
* @param arr 给定数组
* @param index 当前处理下标
* @param rest 剩余累加和
* @param picks 挑选的值
* @return 最接近中间数的累加和
*/
private static int execute(int[] arr, int index, int rest, int picks) {
// 处理到最后一个值
if(index == arr.length) {
// 如果个数刚好结束则返回0,否则返回无效(-1)
return picks == 0 ? 0 : -1;
}
// 不要当前值
int p1 = execute(arr, index + 1, rest, picks);
// 要当前值
int next = -1;
int p2 = -1;
// 只有当前值小于等于剩余中间值是才能要当前值
if(arr[index] <= rest) {
// 递归要后面的值
next = execute(arr, index + 1, rest - arr[index], picks - 1);
// 值有效时才进行值累加(无效值过滤)
if(next != -1) {
p2 = arr[index] + next;
}
}
// 获取最接近中间值的最大情况
return Math.max(p1, p2);
}
4、动态规划
1、分析递归存在3个可变参数,则利用3维数组作为动态规划表
2、先讲所有格子赋值为-1无效值,因为0是有效值。如果不赋值的话无法区分无效值
3、将基础条件赋值为0
4、将递归转化为动态规划,存在越界情况调整一下即可
public static int dp(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
int sum = 0;
for (int i : arr) {
sum += i;
}
int n = arr.length;
// 当前已经除以2,下面不用在除
sum = sum / 2;
int pick = n + 1 / 2;
int[][][] dp = new int[n + 1][sum + 1][pick + 1];
// 将所有值置为无效
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= sum; j++) {
for (int k = 0; k <= pick; k++) {
dp[i][j][k] = -1;
}
}
}
// base case赋值
for (int i = 0; i <= sum; i++) {
dp[n][i][0] = 0;
}
for (int index = n - 1; index >= 0 ; index--) {
for (int rest = 0; rest <= sum; rest++) {
for (int picks = 0; picks <= pick; picks++) {
// 不要当前值
int p1 = dp[index + 1][rest][picks];
// 要当前值
int next = -1;
int p2 = -1;
// 只有当前值小于等于剩余中间值是才能要当前值
if(picks - 1 >= 0 && arr[index] <= rest) {
// 递归要后面的值
next = dp[index +1][rest - arr[index]][picks - 1];
// 值有效时才进行值累加(无效值过滤)
if(next != -1) {
p2 = arr[index] + next;
}
}
// 获取最接近中间值的最大情况
dp[index][rest][picks] = Math.max(p1, p2);
}
}
}
// 偶数
if((arr.length & 1) == 0) {
return dp[0][sum][arr.length / 2];
}
// 奇数
return Math.max(dp[0][sum][arr.length / 2],
dp[0][sum][arr.length / 2 + 1]);
}
总结
1、什么暴力递归可以继续优化:有重复子问题的解,如果每一个子问题都是不同的解则无法优化
2、暴力递归和动态规划的关系:有重复调用才可以优化成动态规划,任何动态规划都对应一个有重复过程的暴力递归
3、如何写动态规划:从尝试开始,写出暴力递归后进行动态规划优化
4、如何找到某个问题的动态规划方式:
- 设计暴力递归(四种常见模型)
- 分析是否存在重复值
- 记忆化搜索-> 严格表结构动态规划
- 看是否能继续优化(优化枚举行为)
5、暴力递归原则
- 根据可变参数设计动态规划表,可变参数一定不要比int类型更复杂
- 如果上一点违背了,需确保单一类型可变(贴纸问题,string类型)
- 违背原则1,不违反原则2,只需做记忆化搜索
- 可变参数格式,经可能的少
6、暴力递归代码编写
- 尽量不违反原则的情况下进行暴力尝试
- 如果找到暴力尝试不符合原则,则找其他原则
- 突破设计原则的题特别难,概率5%
7、常见的4种尝试模型
- 从左往右尝试模型
- 范围上的尝试模型
- 多样本位置对应尝试模型
- 寻找业务限制的尝试模型
8、分析重复解:找具体的例子构建重复解
9、暴力递归到动态规划的套路
- 找到不违反原则的暴力递归,且存在解的重复调用(关键)
- 分析可变参数,以及参数的变化范围(确定表和表的大小)
- 记忆化搜索就是缓存
- 定义动态规划表大小,分析位置依赖顺序,之后从基础条件填写
- 对枚举行为进行优化
10、动态规划的进一步优化
- 空间压缩
- 状态化简
- 四边形不等式
- 其他优化技巧
二十一、N皇后问题(例外)
没办法优化为动态规划的题目
1、题目
N皇后问题是指在N*N的棋盘上要摆N个皇后,要求任何两个皇后不同行、不同列, 也不在同一条斜线上
给定一个整数n,返回n皇后的摆法有多少种。
n=1,返回1。
n=2或3,2皇后和3皇后问题无论怎么摆都不行,返回0。
n=8,返回92
2、思路
1、一行填一个皇后,这样就不用考虑不同行
2、第一行填好后,填第二行时判断是否符合规则。[[a,b],[c,d]] - 利用一维数组即可表示
- 第二行的列等于第一行的列则不符合(b == d)
- 第一行的行减去第二行的行的绝对值, 等于第一行列减去第二行的列的绝对值则不符合(|a-c| == |b-d|)
3、递归
public static int num(int n) {
if(n < 1) {
return 0;
}
int[] record = new int[n];
return process(record, 0, n);
}
/**
* 获取当前位置后面放位置的所有情况数
*
* @param record 存储所有行皇后位置(一维数组存储列,下标代表行)
* @param index 在index行放皇后,所有列都尝试
* @param n 放后数量
* @return 当前下标后面放位置的所有情况数
*/
private static int process(int[] record, int index, int n) {
// 能到达最后位置,则发现一种有效方法
if(index == n) {
return 1;
}
int res = 0;
// 从左往右尝试所有的列
for (int i = 0; i < n; i++) {
// 判断符合规则,则进行下一行处理
if(isValid(record, index, i)) {
// 记录当前位置的列
record[index] = i;
// 当前行选中后,获取后面下一行的所有情况数进行累加
res += process(record, index + 1, n);
}
}
return res;
}
// 校验是否符合规则
private static boolean isValid(int[] record, int index, int i) {
for (int j = 0; j < index; j++) {
if(i == record[j] || Math.abs(record[j] - i) == Math.abs(index - j)) {
return false;
}
}
return true;
}
递归的时间复杂度是n的n次方。
4、优化
利用整数代替一维数组
1、例如第一行第一列放皇后的话。第0行填好后,第1行的列的限制就是第0行的列。第0行的左下没有限制,第0行的右下就限制不能填。则得出结论上一行有皇后位置下一行的列、左下、右下都不能选择
2、后面行选择后就是增加限制,之后一直去更新限制