20_有序表
About 13 minstudyalgorithm
一、AVL
1、介绍
avl树是一种平衡二叉树,在删除和新增元素的时候利用左旋和右旋的方式将树调整平衡,左树的高度和右树的高度差不超过1。这种树的结构建立好之后能有效的提高在应对范围查询时的效率,GPT:
AVL树是一种自平衡的二叉搜索树,它的命名来源于其发明者Adelson-Velskii和Landis。AVL树具有以下特点:
每个节点都有一个表示平衡因子的整数值,用来衡量左右子树的高度差。
AVL树中的任意节点的左右子树高度最多相差1。
当插入或删除操作使得树不再满足平衡条件时,AVL树会通过旋转操作来进行自平衡。
通过对插入和删除操作进行适当的旋转,AVL树能够始终保持近似平衡状态,以提供较快的查找、插入和删除操作。由于其平衡性质,AVL树在大部分情况下能够保证较好的性能,并且没有退化为链表的风险。
需要注意的是,AVL树并非唯一的自平衡二叉搜索树,还存在其他类型的树结构,如红黑树等。这些树结构在实际应用中可以根据具体需求选择合适的数据结构。
2、思路
在新增和删除元素的时候都需要将树调整平衡,最重要的就是平衡逻辑
1、左旋和右旋就是将左子节点或者右子节点变为当前root节点,改变指针指向即可
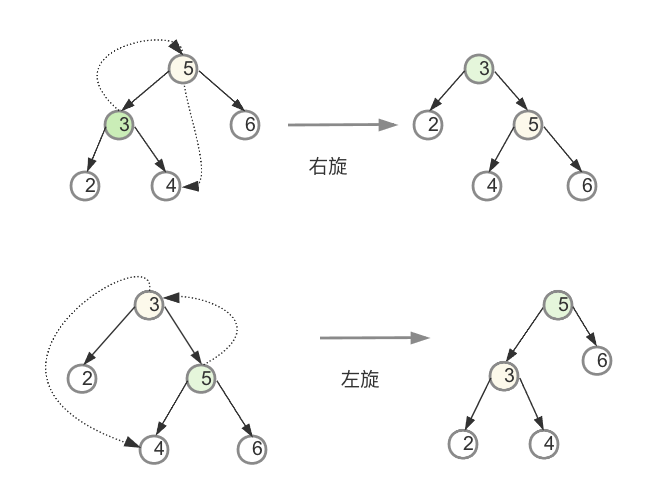
2、调整平衡的主要逻辑是判断左树和右树的高度差大于1时则调整对应子节点
- 左树高
- 左树的左子节点大于等于左树的右子节点:右旋
- 左树的左子节点小于左树的右子节点:左树的左子节点左旋后在右旋
- 右树高
- 左树高度大于右树,则当前节点左旋
- 左树高度小于右树,右树右旋后当前节点左旋
3、删除节点的逻辑场景也比较多
- 删除key大于当前节点则去右边删除节点
- 删除key小于当前节点则去左边删除节点
- 等于当前key则需要判断当前节点的左右子节点是否存在,相应处理后将树调平即可
- 左右子节点都不存在则直接删除
- 只存在左节点则将当前节点指向左节点
- 只存在右节点则将当前节点指向右节点
- 两个都存在:用临时节点记录最左节点,之后删除最左节点后。当前节点赋值为临时节点
3、代码
// avl树
public static class AVLTreeMap<K extends Comparable<K>, V> {
private AVLNode<K, V> root;
public int size;
public AVLTreeMap() {
this.root = null;
this.size = 0;
}
// 获取大小
public int size() {
return size;
}
// 判断关键字是否包含
public boolean containsKey(K k) {
if(k == null) {
return false;
}
AVLNode<K, V> lastIndex = findLastIndex(k);
return lastIndex != null && k.compareTo(lastIndex.k) == 0 ? true: false;
}
// 往树里面添加值
public void put(K k, V v) {
if(k == null) {
return;
}
AVLNode<K, V> lastIndex = findLastIndex(k);
if(lastIndex != null && k.compareTo(lastIndex.k) == 0) {
lastIndex.v= v;
} else {
size++;
root = add(root, k, v);
}
}
// 删除key
public void remove(K key) {
if (key == null) {
return;
}
if (containsKey(key)) {
size--;
// 重新将root指向一下,可能删除头
root = delete(root, key);
}
}
// 获取元素
public V get(K key) {
if (key == null) {
return null;
}
AVLNode<K, V> lastNode = findLastIndex(key);
if (lastNode != null && key.compareTo(lastNode.k) == 0) {
return lastNode.v;
}
return null;
}
// 获取第一个元素,最左节点
public K firstKey() {
if (root == null) {
return null;
}
AVLNode<K, V> cur = root;
while (cur.l != null) {
cur = cur.l;
}
return cur.k;
}
// 获取最后一个元素,最右节点
public K lastKey() {
if (root == null) {
return null;
}
AVLNode<K, V> cur = root;
while (cur.r != null) {
cur = cur.r;
}
return cur.k;
}
// 返回小于或等于给定键的最大键,如果没有这样的键,则null
public K floorKey(K k) {
if(k == null){
return null;
}
AVLNode<K,V> result = null;
AVLNode<K,V> cur = root;
while (cur != null) {
if(k.compareTo(cur.k) == 0) {
result = cur;
break;
}
// 小于k的则往左找,否则往右找
if(k.compareTo(cur.k) < 0) {
cur = cur.l;
} else {
result = cur;
cur=cur.r;
}
}
return result == null ? null : result.k;
}
// 返回大于或等于给定键的最小键,如果没有这样的键,则null
public K ceilingKey(K key) {
if(key == null){
return null;
}
AVLNode<K, V> result = null;
AVLNode<K, V> cur = root;
while (cur != null) {
if (key.compareTo(cur.k) == 0) {
result = cur;
break;
} else if (key.compareTo(cur.k) < 0) {
result = cur;
cur = cur.l;
} else {
cur = cur.r;
}
}
return result == null ? null : result.k;
}
// 右旋
private AVLNode<K, V> rightRotate(AVLNode<K, V> cur) {
AVLNode<K, V> left = cur.l;
// 旋转前左节点指向旋转后的右节点
cur.l = left.r;
// 旋转后的右节点指向旋转前的节点
left.r = cur;
// 计算的高度,左右两边最大的高度加一
setHeight(cur);
setHeight(left);
return left;
}
// 左旋
private AVLNode<K,V> leftRotate(AVLNode<K, V> cur) {
AVLNode<K,V> right = cur.r;
cur.r = right.l;
right.l = cur;
// 计算高度
setHeight(cur);
setHeight(right);
return right;
}
// AVL保持平衡
private AVLNode<K, V> maintain(AVLNode<K, V> cur) {
if(cur == null) {
return null;
}
int lh = cur.l != null ? cur.l.height : 0;
int rh = cur.r != null ? cur.r.height : 0;
// 左树和右树的高度大于1才进行调整
if(Math.abs(lh - rh) < 2) {
return cur;
}
// 左树高
if(lh > rh) {
int llh = cur.l != null && cur.l.l != null ? cur.l.l.height : 0;
int lrh = cur.l != null && cur.l.r != null ? cur.l.r.height : 0;
// 左树高度大于右树,则当前节点右旋
if(llh >= lrh) {
cur = rightRotate(cur);
}
// 左树高度小于右树,左树左旋后当前节点右旋
else {
cur.l = leftRotate(cur.l);
cur = rightRotate(cur);
}
}
// 右树高
else {
int rlh = cur.r != null && cur.r.l != null ? cur.r.l.height : 0;
int rrh = cur.r != null && cur.r.r != null ? cur.r.r.height : 0;
// 左树高度大于右树,则当前节点左旋
if(rrh >= rlh) {
cur = leftRotate(cur);
}
// 左树高度小于右树,右树右旋后当前节点左旋
else {
cur.r = rightRotate(cur.r);
cur = leftRotate(cur);
}
}
return cur;
}
// 给节点设置高度
private void setHeight(AVLNode<K, V> cur) {
// 计算的高度,左右两边最大的高度加一
cur.height = Math.max(cur.l == null ? 0 : cur.l.height, cur.r == null ? 0 : cur.r.height) + 1;
}
// 往AVL节点添加值
private AVLNode<K,V> add(AVLNode<K, V> cur, K k, V v) {
if(cur == null) {
return new AVLNode<>(k, v);
}
// 增加的值小于当前节点,放左边
if(k.compareTo(cur.k) < 0) {
cur.l = add(cur.l, k, v);
}
// 放右边
else {
cur.r = add(cur.r, k, v);
}
setHeight(cur);
return maintain(cur);
}
// 删除k节点,返回删除的节点
private AVLNode<K, V> delete(AVLNode<K, V> cur, K k) {
// 大于当前节点去右边删除
if(k.compareTo(cur.k) > 0) {
cur.r = delete(cur.r, k);
setHeight(cur);
return maintain(cur);
}
// 小于当前节点则去左边删除
if(k.compareTo(cur.k) < 0) {
cur.l = delete(cur.l, k);
setHeight(cur);
return maintain(cur);
}
// 删除的节点没有左右子节点
if(cur.l == null && cur.r == null) {
cur = null;
return null;
}
// 存在左边的子节点
if(cur.l != null && cur.r == null) {
cur = cur.l;
setHeight(cur);
return maintain(cur);
}
// 存在右边的子节点
if(cur.l == null && cur.r != null ) {
cur = cur.r;
setHeight(cur);
return maintain(cur);
}
// 左右两边都存在子节点
AVLNode<K, V> des = cur.r;
// 获取当前右节点的最左节点
while (des.l != null) {
des = des.l;
}
// 删除最左节点后,将树调平衡
cur.r = delete(cur.r, des.k);
// 替换当前节点
des.l = cur.l;
des.r = cur.r;
cur = des;
setHeight(cur);
return maintain(cur);
}
// 通过key检索到节点
private AVLNode<K, V> findLastIndex(K k) {
AVLNode<K, V> pre = root;
AVLNode<K, V> cur = root;
while (cur != null) {
pre = cur;
if(k.compareTo(cur.k) == 0) {
break;
}
// 小于k则左树寻找
if(k.compareTo(cur.k) < 0) {
cur = cur.l;
}
// 否则右树找
else {
cur = cur.r;
}
}
return pre;
}
}
// avl节点
public static class AVLNode<K extends Comparable<K>, V> {
public K k;
public V v;
public AVLNode<K, V> l;
public AVLNode<K, V> r;
public int height;
public AVLNode(K key, V val) {
this.k = key;
this.v = val;
height = 1;
}
}
二、SizeBalansed
1、介绍
SizeBalansedTree是通过用树的大小来作为维持树平衡的依据,AVL是用树的高度来平衡树,AVL更加的严格。SBT在删除key的时候可以不用调整树平衡,在增加树key的时候会迅速调平。GPT:
“Size-Balanced Tree” (SBT) 和 AVL 树是两种用于实现自平衡二叉搜索树的数据结构。
Size-Balanced Tree 是一种自平衡二叉搜索树,它通过维护每个节点的子树大小来保持平衡。在 SBT 中,每个节点都包含一个额外的属性,即其子树的大小。通过动态调整节点在树中的位置,使得左子树和右子树的大小相对平衡,从而实现整个树的平衡。SBT 支持在 O(log n) 的时间内执行搜索、插入和删除操作。
AVL 树是另一种自平衡二叉搜索树,它通过调整节点的高度来保持平衡。在 AVL 树中,每个节点都包含一个平衡因子,即左子树的高度减去右子树的高度。通过旋转操作和调整平衡因子,AVL 树保持所有节点的平衡因子在 {-1, 0, 1} 范围内,从而实现整个树的平衡。AVL 树也能够在 O(log n) 的时间内执行搜索、插入和删除操作。
两种数据结构的主要区别在于平衡条件的不同。SBT 使用子树大小来平衡树,而 AVL 树使用节点高度来平衡树。另外,SBT 相对于 AVL 树有更低的调整代价,因为它只需要维护子树大小而不是节点高度。然而,AVL 树的平衡条件更为严格,可以提供更加均衡的树结构。
选择使用哪种自平衡二叉搜索树取决于具体的应用场景和需求。如果对树的平衡要求比较高且对性能稍作妥协,AVL 树是一个不错的选择。如果对调整代价更为敏感且对树的平衡要求不那么严格,SBT 可能更适合。
Size-Balanced Tree
Size-Balanced Tree(SBT)是一种自平衡二叉搜索树,旨在通过维护节点的子树大小来实现平衡。
在SBT中,每个节点都有一个额外的属性,即其子树的大小。节点的子树大小是指以该节点为根的子树中包含的节点总数。通过在插入、删除和旋转操作中更新节点的子树大小属性,SBT可以保持整个树的平衡。
SBT的平衡条件是,对于任意节点,其左子树的大小至少为其右子树大小的一半,而且右子树的大小至多为其左子树大小的两倍。这种平衡条件保证了树的高度相对平衡,从而保证了搜索、插入和删除操作的较好性能。
与其他自平衡二叉搜索树(例如AVL树或红黑树)相比,SBT的维护代价较低。因为平衡条件相对宽松,SBT往往会调整更少的节点,这导致了更高的插入和删除性能。
SBT在某些特定场景下表现良好,特别是在频繁进行插入和删除操作的情况下。然而,它并不是通用的数据结构,适用于所有情况。因此,在选择数据结构时,需要根据具体的应用需求和性能要求进行评估和决策。
2、思路
1、左旋和右旋的方式和AVL一致,只是将高度替换为大小
2、调整平衡的时候每次左旋或右旋之后都递归调整平衡
3、删除节点时可以不调整平衡,增加节点时会迅速调平
3、代码
public static class SizeBalancedTreeMap<K extends Comparable<K>,V> {
private SBTNode<K, V> root;
// 左旋
private SBTNode<K, V> rightRotate(SBTNode<K, V> cur) {
SBTNode<K, V> l = cur.l;
cur.l = l.r;
l.r = cur;
l.size = cur.size;
cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
return l;
}
// 右旋
private SBTNode<K, V> leftRotate(SBTNode<K, V> cur) {
SBTNode<K, V> r = cur.r;
cur.r = r.l;
r.l = cur;
r.size = cur.size;
cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
return r;
}
private SBTNode<K,V> maintain(SBTNode<K, V> cur) {
if(cur == null) {
return null;
}
// 左树大小
int ls = cur.l != null ? cur.l.size : 0;
int lls = cur.l !=null && cur.l.l != null ? cur.l.l.size : 0;
int lrs = cur.l != null && cur.l.r != null ? cur.l.r.size : 0;
// 右树大小
int rs = cur.r != null ? cur.r.size : 0;
int rls = cur.r != null && cur.r.l != null ? cur.r.l.size : 0;
int rrs = cur.r != null && cur.r.r != null ? cur.r.r.size : 0;
// 左左树的树立大于右树的数量
if(lls > rs) {
cur = rightRotate(cur);
// 右边调整平衡
cur.r = maintain(cur.r);
cur = maintain(cur);
return cur;
}
// 左右树大于右树
if(lrs > rs) {
cur.l = leftRotate(cur.l);
cur = rightRotate(cur);
// 调整平衡
cur.l = maintain(cur.l);
cur.r = maintain(cur.r);
cur = maintain(cur);
return cur;
}
if(rrs > ls) {
cur = leftRotate(cur);
// 左边调整平衡
cur.l = maintain(cur.l);
cur = maintain(cur);
return cur;
}
if(rls > ls) {
cur.r = rightRotate(cur.r);
cur = leftRotate(cur);
// 调整平衡
cur.l = maintain(cur.l);
cur.r = maintain(cur.r);
cur = maintain(cur);
return cur;
}
return cur;
}
// 找到树上面k相等的值
private SBTNode<K, V> findLastIndex(K k) {
SBTNode<K, V> pre = root;
SBTNode<K, V> cur = root;
while (cur != null) {
pre = cur;
// 相等
if(k.compareTo(cur.k) == 0) {
break;
}
// 去左边找
else if (k.compareTo(cur.k) < 0) {
cur = cur.l;
}
// 去右边
else {
cur = cur.r;
}
}
return pre;
}
// 离当前值较小的值
private SBTNode<K, V> findLastNoSmallIndex(K key) {
SBTNode<K, V> ans = null;
SBTNode<K, V> cur = root;
while (cur != null) {
if (key.compareTo(cur.k) == 0) {
ans = cur;
break;
} else if (key.compareTo(cur.k) < 0) {
ans = cur;
cur = cur.l;
} else {
cur = cur.r;
}
}
return ans;
}
// 离当前值较大的值
private SBTNode<K, V> findLastNoBigIndex(K key) {
SBTNode<K, V> ans = null;
SBTNode<K, V> cur = root;
while (cur != null) {
if (key.compareTo(cur.k) == 0) {
ans = cur;
break;
} else if (key.compareTo(cur.k) < 0) {
cur = cur.l;
} else {
ans = cur;
cur = cur.r;
}
}
return ans;
}
// 添加节点
private SBTNode<K, V> add(SBTNode<K, V> cur, K k, V v) {
if(cur == null ) {
return new SBTNode<>(k, v);
}
cur.size++;
// 左边树添加元素
if(k.compareTo(cur.k) < 0){
cur.l = add(cur.l, k, v);
}
// 右边树添加元素
else {
cur.r = add(cur.r, k, v);
}
return maintain(cur);
}
// 删除元素
private SBTNode<K, V> delete(SBTNode<K, V> cur, K k) {
cur.size--;
// 左边树删除元素
if(k.compareTo(cur.k) < 0) {
cur.l = delete(cur.l, k);
return cur;
}
// 右边树删除元素
if(k.compareTo(cur.k) > 0) {
cur.r = delete(cur.r, k);
return cur;
}
// 相等则删除当前元素
// 左右节点都不为空
if(cur.l == null && cur.r == null) {
cur = null;
return null;
}
// 只有左节点,则cur直接指向左节点
if(cur.l != null && cur.r == null) {
cur = cur.l;
return cur;
}
// 只有右节点,则cur直接指向右节点
if(cur.l == null && cur.r != null) {
cur = cur.r;
return cur;
}
// 删除最左节点后,将树调平衡
SBTNode<K, V> des = cur.r;
SBTNode<K, V> pre = null;
des.size--;
while (des.l != null) {
pre = des;
des = des.l;
des.size--;
}
if(pre != null) {
pre.l = des.r;
des.r = cur.r;
}
des.l = cur.l;
des.size = des.l.size + (des.r == null ? 0 : des.r.size) + 1;
cur = des;
return cur;
}
// 获取
private SBTNode<K, V> getIndex(SBTNode<K, V> cur, int kth) {
// 大小匹配到
if (kth == (cur.l != null ? cur.l.size : 0) + 1) {
return cur;
}
// 小于当前树大小,往左边找
else if (kth <= (cur.l != null ? cur.l.size : 0)) {
return getIndex(cur.l, kth);
}
// 大于树大小,往右边找
else {
return getIndex(cur.r, kth - (cur.l != null ? cur.l.size : 0) - 1);
}
}
// 获取树大小
public int size() {
return root == null ? 0 : root.size;
}
// 是否包含key
public boolean containsKey(K key) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
SBTNode<K, V> lastNode = findLastIndex(key);
return lastNode != null && key.compareTo(lastNode.k) == 0 ? true : false;
}
// 新增k v, 修改也是直接put
public void put(K key, V value) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
// 判断值是否窜
SBTNode<K, V> lastNode = findLastIndex(key);
// 存在则进行修改
if (lastNode != null && key.compareTo(lastNode.k) == 0) {
lastNode.v = value;
}
// 不存在则进行新增
else {
root = add(root, key, value);
}
}
// 删除
public void remove(K key) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
// 判断存在则删除
if (containsKey(key)) {
root = delete(root, key);
}
}
// 通过索引获取k
public K getIndexKey(int index) {
if (index < 0 || index >= this.size()) {
throw new RuntimeException("invalid parameter.");
}
return getIndex(root, index + 1).k;
}
// 通过索引获取v
public V getIndexValue(int index) {
if (index < 0 || index >= this.size()) {
throw new RuntimeException("invalid parameter.");
}
return getIndex(root, index + 1).v;
}
// 通过k获取v
public V get(K key) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
SBTNode<K, V> lastNode = findLastIndex(key);
if (lastNode != null && key.compareTo(lastNode.k) == 0) {
return lastNode.v;
} else {
return null;
}
}
// 获取第一个key
public K firstKey() {
if (root == null) {
return null;
}
SBTNode<K, V> cur = root;
// 获取树的最左
while (cur.l != null) {
cur = cur.l;
}
return cur.k;
}
// 获取最后一个key
public K lastKey() {
if (root == null) {
return null;
}
SBTNode<K, V> cur = root;
// 获取树的最右
while (cur.r != null) {
cur = cur.r;
}
return cur.k;
}
// 返回小于或等于给定键的最大键,如果没有这样的键,则null
public K floorKey(K key) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
SBTNode<K, V> lastNoBigNode = findLastNoBigIndex(key);
return lastNoBigNode == null ? null : lastNoBigNode.k;
}
// 返回大于或等于给定键的最小键,如果没有这样的键,则null
public K ceilingKey(K key) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
SBTNode<K, V> lastNoSmallNode = findLastNoSmallIndex(key);
return lastNoSmallNode == null ? null : lastNoSmallNode.k;
}
}
三、SkipList跳表
1、介绍
map中进行大于小于操作,增删改查都是O(logn)